

E (nombre) L’aire sous l’hyperbole est égale à 1 sur l’intervalle [1, e].
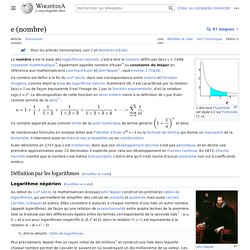
Le nombre e[a] est la base des logarithmes naturels, c'est-à-dire le nombre défini par ou de façon équivalente il est l'image de 1 par la fonction exponentielle, d'où la notation et dans de nombreuses formules en analyse telles l'identité d'Euler ou la formule de Stirling qui donne un équivalent de la factorielle.
Il intervient aussi en théorie des probabilités ou en combinatoire. Euler démontre en 1737 que e est irrationnel, donc que son développement décimal n'est pas périodique, et en donne une première approximation avec 23 décimales. Plus précisément, Napier fixe un rayon initial de dix millions[d] et construit une liste dans laquelle chaque nombre permet de calculer le suivant en lui soustrayant un dix-millionième de sa valeur. Or l'approximation affine du logarithme naturel en 1 permet d'approcher ln(1 − 10−7) par −10−7 avec une précision de l'ordre de 10−14, soit 7 chiffres significatifs. . Donc, Ainsi, n!
. Identité d'Euler. Un article de Wikipédia, l'encyclopédie libre.
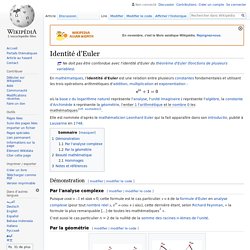
En mathématiques, l'identité d'Euler est une relation entre plusieurs constantes fondamentales et utilisant les trois opérations arithmétiques d'addition, multiplication et exponentiation : Elle est nommée d'après le mathématicien Leonhard Euler qui la fait apparaître dans son Introductio, publié à Lausanne en 1748. Démonstration[modifier | modifier le code] Par l'analyse complexe[modifier | modifier le code] Puisque cosπ = –1 et sinπ = 0, cette formule est le cas particulier x = π de la formule d'Euler en analyse complexe (pour tout nombre réel x, eix = cosx + i sinx), cette dernière étant, selon Richard Feynman, « la formule la plus remarquable […] de toutes les mathématiques[2] ». C'est aussi le cas particulier n = 2 de la nullité de la somme des racines n-ièmes de l'unité.
Par la géométrie[modifier | modifier le code] Juxtaposition de 8 triangles rectanglesJuxtaposition de 16 triangles rectangles. Nombre algébrique. Un article de Wikipédia, l'encyclopédie libre.
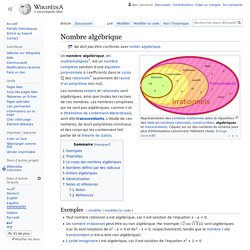
Entier algébrique. Pour les articles homonymes, voir Entier.
En mathématiques, un entier algébrique est un élément d'un corps de nombres qui y joue un rôle analogue à celui d'un entier relatif dans le corps des nombres rationnels. L'étude des entiers algébriques est à la base de l'arithmétique des corps de nombres, et de la généralisation dans ces corps de notions comme celles de nombre premier ou de division euclidienne. Par définition, un entier algébrique est une racine d'un polynôme unitaire à coefficients dans ℤ. Par exemple, le nombre 1 + √3 est un entier algébrique, car il est une racine du polynôme unitaire à coefficients entiers X2 – 2X – 2. Les nombres de la forme a + bi où a et b sont des entiers relatifs et où i désigne une racine du polynôme X2 + 1 sont aussi des entiers algébriques particuliers ; ils sont appelés entiers de Gauss.
Entier quadratique. Pour les articles homonymes, voir Entier.
En mathématiques, un entier quadratique est un nombre complexe, racine d'un polynôme unitaire du second degré à coefficients entiers. La notion de nombre algébrique de degré inférieur ou égal à 2 est plus générale. Elle correspond encore à un nombre complexe, racine d'un polynôme du second degré à coefficients rationnels. Ces nombres particuliers disposent de propriétés algébriques. Nombre de Liouville. En mathématiques, et plus précisément en théorie des nombres, un nombre de Liouville est un nombre réel x ayant la propriété suivante : pour tout entier n > 0, il existe des entiers qn > 1 et pn tels que 0 < |x – pn/qn| < 1/qnn ou, ce qui est équivalent : pour tout entier n et tout réel A > 0, il existe des entiers q > 0 et p tels que 0 < |x – p/q| < A/qn.
Constante de Liouville[modifier | modifier le code] Pour illustrer son théorème, Liouville donne un procédé général de construction de tels nombres à l'aide de la théorie des fractions continues, ainsi que des exemples, mais indique une méthode plus simple : par exemple, pour tout entier est un nombre de Liouville. La constante de Liouville correspond au cas . Nombre normal. Définitions[modifier | modifier le code] Notons l'ensemble des chiffres en base b, et soit x un nombre réel.
Si s est une suite finie d'éléments de A, notons N(s, n) le nombre d'apparitions de la suite s parmi les n premiers chiffres après la virgule du développement propre de x en base b. Nombre univers. Un article de Wikipédia, l'encyclopédie libre.
Tout nombre normal est un nombre univers, mais la réciproque est fausse : dans un nombre normal, chaque séquence apparaît une infinité de fois selon une statistique équirépartie ; dans un nombre univers, on ne garantit que l'apparition de chaque séquence, et aucune propriété statistique sur leurs fréquences relatives. Constante de Champernowne. En mathématiques, la constante de Champernowne, noté est un nombre réel transcendant, nommé ainsi en l'honneur du mathématicien D.
G. Champernowne. Bailey–Borwein–Plouffe formula. The Bailey–Borwein–Plouffe formula (BBP formula) is a spigot algorithm for computing the nth binary digit of pi (symbol: π) using base 16 math.
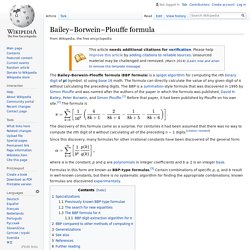
The formula can directly calculate the value of any given digit of π without calculating the preceding digits. The BBP is a summation-style formula that was discovered in 1995 by Simon Plouffe and was named after the authors of the paper in which the formula was published, David H. Bailey, Peter Borwein, and Simon Plouffe.[1] Before that paper, it had been published by Plouffe on his own site.[2] The formula is The discovery of this formula came as a surprise. For centuries it had been assumed that there was no way to compute the nth digit of π without calculating all of the preceding n − 1 digits. Since this discovery, many formulas for other irrational constants have been discovered of the general form where α is the constant, p and q are polynomials in integer coefficients and b ≥ 2 is an integer base.
Specializations[edit] can be written as.