

Mathématiques du jonglage. Vincent Pantaloni Modélisation Les univers du cirque et des mathématiques semblent être parallèles.
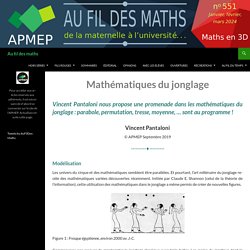
Et pourtant, l’art millénaire du jonglage recèle des mathématiques variées découvertes récemment. Initiée par Claude E. Shannon (celui de la théorie de l’information), cette utilisation des mathématiques dans le jonglage a même permis de créer de nouvelles figures. Commençons par essayer de représenter le jonglage classique avec trois balles.
Si on regarde la même scène du dessus, les balles vont de droite à gauche puis de gauche à droite. Ci-dessous, on a déroulé le mouvement sur une période, et on observe un motif de tresse à trois brins. Théorème de Shannon On sait peu que Claude E. . On utilisera le théorème de Shannon pour déterminer à quelle hauteur il faut lancer les balles pour un jonglage régulier avec un nombre donné de balles. Démonstration : on utilise la représentation en tresse, avec le temps s’écoulant vers le bas. En divisant de part et d’autre par , on obtient : Siteswap. Tangente Fractales. Tangente HS n°23. Les fractales. D'autres images en bas de page Le mot "fractale" vient du latin "fractus" qui signifie "brisé".
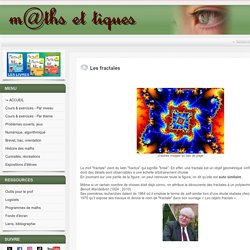
En effet, une fractale est un objet géométrique «infiniment morcelé» dont des détails sont observables à une échelle arbitrairement choisie. En zoomant sur une partie de la figure, on peut retrouver toute la figure, on dit qu’elle est auto similaire. Même si un certain nombre de choses était déjà connu, on attribue la découverte des fractales à un polytechnicien français, Benoît Mandelbrot (1924 ; 2010). Ses premières recherches datent de 1964 où il emploie le terme de self-similar lors d'une étude réalisée chez IBM. La manière la plus simple d’obtenir une fractale, c’est de la trouver dans la nature. Avec deux miroirs mis face à face vous pouvez aussi vous amuser à créer un objet fractal. Quelques artistes nous offrent aussi de belles réalisations de fractales, comme M.C.Escher ou P.Raedschelders. Le flocon de neige s’obtient lorsque la figure initiale est un triangle équilatéral. Fractales. Representation de l espace. De nouvelles perspectives.
Les recherches des peintres de la Renaissance en Italie visant à produire des représentations plus réalistes dans les tableaux ont ouvert des perspectives nouvelles aux géomètres.
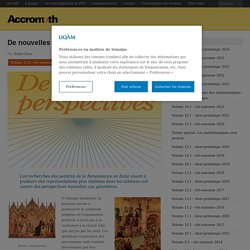
Martini, L’Annonciation Duccio, L’Entrée à Jérusalem À l’époque médiévale, la peinture servait à promouvoir le sentiment religieux et l’organisation picturale n’avait pas à se conformer à la réalité telle que perçue par les sens. Les grandeurs respectives des personnages sont souvent déterminées par leur importance dans le drame chrétien plutôt que leur position dans l’espace. L’Annonciation de Simone Martini (1284-1344), réalisée pour la cathédrale de Sienne, est un exemple de peinture médiévale.
Giotto, La Cène Au début du quatorzième siècle, l’organisation picturale a commencé à évoluer. La deuxième moitié du quatorzième siècle ne fut pas très propice aux développements, tant artistiques que scientifiques, alors que la peste noire décimant la population en Europe. Images des mathématiques. Bernar Venet est un artiste plasticien français, né en 1941 à Château-Arnoux-Saint-Auban dans les Alpes-de-Haute-Provence.

Il réside aux États-Unis où il s’est fait connaître pour ses sculptures d’acier et ses dessins. Site officiel. Vue des peintures murales, 2002 Acrylique sur mur au Ludwig Museum, Coblence, Allemagne, 2002. 1- Alors que vous n’aviez cessé depuis de nombreuses années de faire quasi exclusivement que de la sculpture, voilà que vous multipliez un nouveau type de travail qui en appelle tant à la peinture qu’aux mathématiques et que vous nommez des « peintures murales ».
De manière très naturelle. Arcs en désordre : 4 Arcs x 5, 2007 Acier Cor-ten, 410 x 415 x 90 cm chacun. 2- C’est un type de travail qui est aux antipodes de votre sculpture et qui rappelle vos œuvres du début. Seule une approche superficielle donnera l’impression d’un retour en arrière. 3- A quoi correspond selon vous une telle résurgence ? Accident, 1996 Acier laminé.