

Avant propos – Introduction-Avant propos – Introduction. Les termes de Mécanique Quantique, Physique quantique et Chimie quantique sont des termes qui effraient souvent le lecteur.

S'il est vrai que le développement des théories requiert des notions de mathématiques relativement avancées et parfois une certaine nécessité d'abstraction, il n'en demeure pas moins que les développements récents des logiciels rendent désormais accessibles une grande partie de leur domaine d'application. En particulier, la Chimie quantique, aussi dénommée Chimie théorique ou Modélisation moléculaire, a fait l'objet de nombreux développements logiciels qui permettent à un chimiste avisé de réaliser des calculs plus ou moins compliqués et surtout d'en tirer des résultats qui lui permettront une analyse affinée du système moléculaire étudié. Toutefois, les thèmes choisis ici, restent dans le cadre d'une progression pédagogique touchant des thèmes allant de la première année universitaire jusqu'à la troisième. A quoi sert un calcul de Chimie quantique ?
Les Orbitales Atomiques-Introduction - Les orbitales Atomiques et Moléculaires. Solutions de l'équation de Schrödinger. L'atome d'hydrogène est le système simple qui permet de décrire aisément le concept fondamental d'orbitale atomique.

Derrière le terme d'orbitale se cache en fait la fonction d'onde, vecteur propre de l'équation de Schrödinger, associée aux mouvements de l'électron dans le champ d'un ou plusieurs protons constituant le noyau. Ce type d'orbitale est nommé orbitale hydrogénoïde. Cette solution qui correspond à un système mono-électronique pourra ensuite être étendu à des systèmes plus complexes présentant un nombre d'électrons plus élevé, moyennant quelques approximations. Nous présenterons ici les approximations essentielles mais surtout les conséquences en termes de construction d'objets (les « bases d'orbitales » atomiques) qui seront utilisées dans le cadre des calculs de chimie quantique. Dans ce chapitre, seront présentés les développements mathématiques permettant d'atteindre cette description.
Les Orbitales Atomiques-L'atome hydrogénoïde. L'étude de l'atome hydrogénoïde se résume donc à l'étude d'un système dans lequel deux particules sont présentes : - un noyau de masse M et de charge +Ze - un électron de masse me et de charge -e L'équation de Schrödinger indépendante du temps s'écrit : Afin de simplifier cette équation, on se ramène au centre de masse du système.
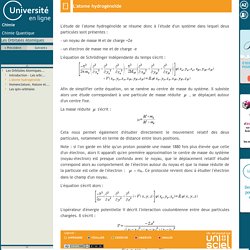
Il subsiste alors une étude correspondant à une particule de masse réduite. Les Orbitales Atomiques-Nomenclature, Nature et Propriétés des solutions obtenues. - Nomenclature : Le nombre quantique n permet de spécifier une couche électronique.
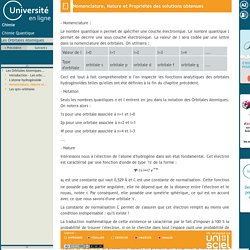
Le nombre quantique l permet de décrire une sous couche électronique. La valeur de l sera codée par une lettre dans la nomenclature des orbitales. On utilisera : Ceci est tout à fait compréhensible si l'on inspecte les fonctions analytiques des orbitales hydrogénoïdes telles qu'elles ont été définies à la fin du chapitre précédent. Les Orbitales Atomiques-Les spin-orbitales. L'électron est une particule chargée en mouvement autour du noyau.

Dans ce cadre, il a été démontré que l'électron possède un moment magnétique permanent, qui est appelé moment magnétique orbital. Le mouvement associé de l'électron est appelé mouvement orbital. Lorsque cet électron est placé dans le champ d'une impulsion magnétique, alors un terme supplémentaire décrivant cette origine magnétique doit être ajouté à l'énergie potentielle de l'électron. Les fonctions propres de l'opérateur Hamiltonien que nous avons décrit précédemment, et qui ne comporte pas de terme magnétique, sont encore fonctions propres de ce nouvel opérateur. Les valeurs propres associées à ces solutions prennent alors la forme : avec m le nombre quantique magnétique. Un niveau caractérisé par le nombre quantique secondaire l va ainsi éclater en 2l+1 sous niveaux correspondant aux différentes valeurs de m (de –l à +l).
Et sont alors les fonctions associées au spin. L'opérateur hamiltonien-Introduction. L'hamiltonien Moléculaire - La construction des orbitales moléculaires – Le cadre du modèle. L'opérateur hamiltonien-La construction de l'Hamiltonien moléculaire et les approximations. Un hamiltonien complet décrivant les particules d'un système moléculaire complexe (plusieurs atomes) peut s'écrire sous la forme simplifiée : avec - T e et T N les expressions décrivant le comportement cinétique des électrons et des noyaux respectivement. - V eN correspond au potentiel attractif ressenti par les électrons placés dans le champ positif des noyaux. - V NN et V ee sont respectivement les potentiels électrostatiques répulsifs noyau-noyau et électron-électron.

-V ext est le potentiel extérieur imprimé par l'environnement sur les particules du système. L'opérateur hamiltonien-Les solutions de l'Hamiltonien moléculaire : les orbitales moléculaires. La méthode LCAO.
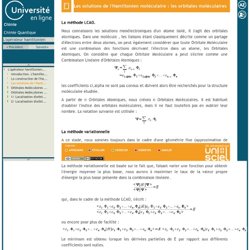
Nous connaissons les solutions monélectroniques d'un atome isolé, il s'agit des orbitales atomiques. Dans une molécule , les liaisons étant classiquement décrite comme un partage d'électrons entre deux atomes, on peut également considérer que toute Orbitale Moléculaire est une combinaison des fonctions décrivant l'électron dans un atome, les Orbitales Atomiques. On considère que chaque Orbitale Moléculaire a peut s'écrire comme une Combinaison Linéaire d'Orbitales Atomiques : les coefficients ci,alpha ne sont pas connus et doivent alors être recherchés pour la structure moléculaire étudiée.
A partir de n Orbitales Atomiques, nous créons n Orbitales Moléculaires. La méthode variationnelle A ce stade, nous sommes toujours dans le cadre d'une géométrie fixe (approximation de Born-Oppenheimer). Qui, dans le cadre de la méthode LCAO, s'écrit : ou encore pour plus de facilité : Pour plus de simplicité, dans la suite du développement, on notera : L'opérateur hamiltonien-Orbitales Moléculaires d'une molécule diatomique homonucléaire. L'opérateur hamiltonien-Orbitales Moléculaires d'une molécule diatomique hétéronucléaire. On suppose que les deux noyaux de deux atomes de type différents sont maintenus à une distance fixe (ce qui revient à appliquer l'approximation de Born-Oppenheimer).
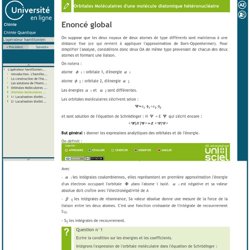
Pour simplifier l'analyse, considérons donc deux OA de même type provenant de chacun des deux atomes et formant une liaison. On notera : atome 1 : orbitale 1, d'énergie 2 : orbitale 2, d'énergie Les énergies. L'opérateur hamiltonien-1/ Localisation d'orbitales - Orbitales localisées du méthane. La molécule de méthane, CH 4 , possède une géométrie tétraédrique qui peut être insérée dans un cube, comme présenté dans la figure ci-dessous : L'atome de carbone occupe le centre du cube alors que les quatre atomes d'hydrogène occupent quatre des huit sommets. Ces derniers sont donc à équidistance de l'atome de carbone. Les orbitales atomiques du carbone jouant dans la construction des orbitales moléculaires sont les orbitales 2sc, 2pxc, 2pyc et 2pzc. Chaque orbitale 1s (notées 1s1, 1s2, 1s3 et 1s4) des atomes d'hydrogène seront également impliquées dans les orbitales moléculaires.
L'opérateur hamiltonien-2/ Localisation d'orbitales - Orbitales localisées de BeH2. Les Orbitales Moléculaires-Introduction : La représentation des Orbitales Atomiques et les Méthodes de résolution de l'équation de Schrödinger. Les deux premiers chapitres nous ont permis de définir la forme des équations et de leurs solutions d'un coté au niveau atomique et de l'autre au niveau moléculaire.
Nous avons pu voir que de nombreuses approximations étaient nécessaires pour obtenir une résolution aisée de l'équation de Schrödinger. Ceci va avoir un impact important sur la précision des résultats obtenus. Malgré tout, les protocoles présentés dans ces deux premiers chapitres doivent être mis en œuvre d'un point de vue calculatoire. Et dans ce cadre, quelques étapes doivent encore être dépassées. Les Orbitales Moléculaires-Les bases d'orbitales atomiques. Les orbitales de Slater Les orbitales hydrogénoïdes sont les solutions de l'équation de Schrödinger appliquées à un système monoélectronique.

L'étude d'un système comportant plusieurs électrons mène à l'introduction d'un potentiel coulombien répulsif électron-électron dans l'écriture de l'Hamiltonien complet, ce qui entraîne de considérables complications pour sa résolution. Afin de rendre cette résolution plus aisée, on applique une approximation considérant les électrons indépendamment les un des autres. Dès lors, l'Hamiltonien complet peut s'écrire comme la somme d'Hamiltoniens mono-électroniques et ses solutions sont alors le produit des orbitales hydrogénoïdes. Ce type de solution ne tient pas compte de la répulsion électronique. Les Orbitales Moléculaires-La Méthode Hatree-Fock.
Nous avions défini un Hamiltonien électronique approché : Le corrolaire de cette approximation est alors que la fonction d'onde totale peut-être considérée comme le produit des solutions mono-électroniques de cette équation On écrit : Malheureusement, cette fonction d'onde ne satisfait pas au principe de Pauli qui stipule que la fonction d'onde décrivant un système multiélectronique doit changer de signe lors de la permutation des coordonnées de deux électrons quelconques. Pour obéir au principe de Pauli, il faut introduire une fonction qui permettra de définir les propriétés de spin. Les différentes méthodes de chimie computationnelle-Introduction à la chimie computationnelle.
Le passage de la théorie à la pratique requiert encore quelques notions. Toutefois, les fondements théoriques dépassant les attendus de ce module, ne seront présentés que les concepts généraux des méthodes que l'on peut mettre en place lors d'un calcul de chimie quantique. Ainsi, seront rappelées ci-après les différentes familles de méthodes utilisables dans le cadre d'une étude d'un système moléculaire par Chimie quantique. Les différents thèmes qui vous sont proposés par la suite reprennent certaines de ces familles de méthodes. Chacune d'entre elle a montré sa force, mais aussi certaines de ses faiblesses, dans le cadre de ces études appliquées. Les méthodes Hartree-Fock et semi-empiriques.
Nous avons vu dans le chapitre précédent, dans le développement de la méthode Hartree-Fock, qu'on est amené à calculer un grand nombre d'intégrale de la forme : étant donné que les intégrales J et K sont développées sur les Orbitales Atomiques du système. Les méthodes semi-empiriques Dans le développement de la méthode Hartree-Fock présenté dans le chapitre précédent, toutes ces intégrales sont calculées, y compris celles impliquant les électrons internes. Dans les méthodes semi-empiriques, ce protocole de calcul va être simplifié en appliquant diverses approximations supplémentaires : la contribution des électrons internes sera négligé les électrons de valence seront représentés par une base minimale de Slater (voir chapitre précédent) certaines intégrales seront évaluées à l'aide de paramètres empiriques la plupart des intégrales multicentriques seront négligées. Les méthodes Hartree-Fock restreintes (RHF et ROHF) et la méthode non-restreinte (UHF)
Les méthodes post-HF. Nous avons vu dans le chapitre précédent que, dans le cadre de la méthode Hatree-Fock, la fonction d'onde était définie par un déterminant de Slater. Les orbitales qui sont utilisées sont des orbitales de Slater qui ont été construites de telle façon à ce que chaque électron ressente un champ moyen provenant des autres électrons. On peut donc en conclure que la méthode Hatree-Fock ne peut pas rendre compte des interactions instantanées des électrons : la méthode Hatree-Fock ne tient pas compte de la corrélation électronique. Pour augmenter la précision de nos calculs, il est donc nécessaire de corriger ou de compléter la méthode Hatree-Fock. De nombreuses méthodes existent, seules certaines d'entre elles vont être décrites ici. Les méthodes de la fonctionnelle de la densité.
La surface d'énergie potentielle. Vers la description de chemins réactionnels-Introduction. Les points caractéristiques d'une surface. Cela signifie que les systèmes moléculaires classiques, tels qu'on va les étudier, vont minimiser leur énergie potentielle en évacuant l'excès sous forme de dissipation (chaleur) ou sous la forme d'une autre énergie (l'énergie cinétique). Par exemple, une bille posée sur le sommet d'une surface concave -initialement avec une énergie potentielle élevée et une énergie cinétique nulle- va rouler pour atteindre le point la plus bas de la surface et ainsi minimiser son énergie potentielle et acquérir de l'énergie cinétique. Caractérisation des points stationnaires dans l'approximation harmonique. Les étapes de la description d'un mécanisme réactionnel. Exercices transverses-Prise en main des logiciels. Prise en main de Gabedit : Orbitales Atomiques / Orbitales Moléculaires. Comparaison entre les approches de type VSEPR et les calculs de chimie quantique.
Effet inductif et effet mésomère. 2.Effet mésomère La mésomérie désigne le fait que des électrons peuvent se délocaliser sur une ou plusieurs liaisons d'une molécule. Dans ce contexte, sa représentation de Lewis n'est plus unique mais résulte d'une combinaison de plusieurs structures dites mésomères. La règle de Walsh. Méthode des fragments. La théorie des orbitales moléculaires est, à ce jour, la théorie la plus aboutie en matière de description de l'infiniment petit. Elle est basée sur l'équation de Schrödinger, qui permet de relier une fonction d'onde, représentant un électron ici, à son énergie.
De par sa grande complexité, il est difficile, voire impossible, de résoudre directement cette équation pour un système moléculaire donné. Nous devons donc utiliser des modèles, développés au cours du XXème siècle, pour pouvoir approcher les OM et les différentes propriétés pouvant être mise en lumière grâce à elles. Il faut cependant garder en mémoire que ces méthodes de résolution, quelles qu'elles soient, ne restent que des approximations des solutions exactes qui ne peuvent être obtenues que par la résolution de l'équation de Schrödinger. Réarrangement Pinacolique.