

The Lab. APMonitor. Advanced process monitor (APMonitor) , is a modeling language for differential and algebraic ( DAE ) equations. [ 1 ] It is a free web-service for solving representations of physical systems in the form of implicit DAE models.
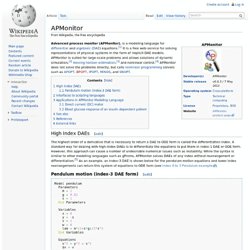
APMonitor is suited for large-scale problems and allows solutions of dynamic simulation, [ 2 ] moving horizon estimation , [ 3 ] and nonlinear control. [ 4 ] APMonitor does not solve the problems directly, but calls nonlinear programming solvers such as APOPT , BPOPT , IPOPT , MINOS , and SNOPT . High Index DAEs [ edit ] The highest order of a derivative that is necessary to return a DAE to ODE form is called the differentiation index .
A standard way for dealing with high-index DAEs is to differentiate the equations to put them in index-1 DAE or ODE form. However, this approach can cause a number of undesirable numerical issues such as instability. Pendulum motion (index-3 DAE form) [ edit ] Interfaces to scripting languages [ edit ] Model motor Parameters ! ! Mathieu function. In mathematics, the Mathieu functions are certain special functions useful for treating a variety of problems in applied mathematics, including: They were introduced by Émile Léonard Mathieu (1868) in the context of the first problem.
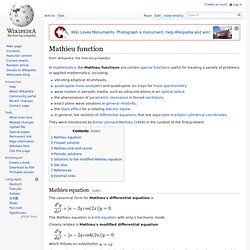
Mathieu equation[edit] The canonical form for Mathieu's differential equation is The Mathieu equation is a Hill equation with only 1 harmonic mode. Closely related is Mathieu's modified differential equation which follows on substitution The two above equations can be obtained from the Helmholtz equation in two dimensions, by expressing it in elliptical coordinates and then separating the two variables.[1] This is why they are also known as angular and radial Mathieu equation, respectively. The substitution transforms Mathieu's equation to the algebraic form This has two regular singularities at Floquet solution[edit] According to Floquet's theorem (or Bloch's theorem), for fixed values of a,q, Mathieu's equation admits a complex valued solution of form where .
Given . Spring pendulum. Inverted pendulum. Balancing cart, a simple robotics system 1976.
A second type of inverted pendulum is a tiltmeter for tall structures, which consists of a wire anchored to the bottom of the foundation and attached to a float in a pool of oil at the top of the structure that has devices for measuring movement of the neutral position of the float away from its original position. Overview[edit] Another way that an inverted pendulum may be stabilized, without any feedback or control mechanism, is by oscillating the support rapidly up and down. This is called Kapitza's pendulum. Double pendulum. A double pendulum consists of two pendulums attached end to end.
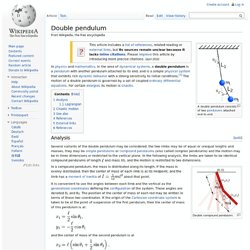
In physics and mathematics , in the area of dynamical systems , a double pendulum is a pendulum with another pendulum attached to its end, and is a simple physical system that exhibits rich dynamic behavior with a strong sensitivity to initial conditions. [ 1 ] The motion of a double pendulum is governed by a set of coupled ordinary differential equations . For certain energies its motion is chaotic . Conical pendulum. A conical pendulum is a weight (or bob ) fixed on the end of a string (or rod) suspended from a pivot.
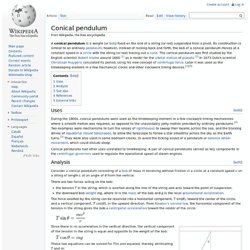
Its construction is similar to an ordinary pendulum ; however, instead of rocking back and forth, the bob of a conical pendulum moves at a constant speed in a circle with the string (or rod) tracing out a cone . The conical pendulum was first studied by the English scientist Robert Hooke around 1660 [ 1 ] as a model for the orbital motion of planets . [ 2 ] In 1673 Dutch scientist Christiaan Huygens calculated its period, using his new concept of centrifugal force .
Later it was used as the timekeeping element in a few mechanical clocks and other clockwork timing devices. [ 3 ] [ 4 ] [ edit ] Uses Conical pendulums had other uses unrelated to timekeeping. Blackburn pendulum. Jacobi elliptic functions. Introduction[edit] Auxiliary rectangle construction There are twelve Jacobian elliptic functions.
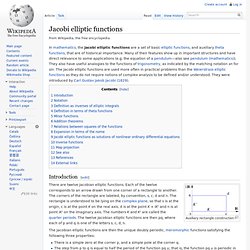
Each of the twelve corresponds to an arrow drawn from one corner of a rectangle to another. The corners of the rectangle are labeled, by convention, s, c, d and n. The rectangle is understood to be lying on the complex plane, so that s is at the origin, c is at the point K on the real axis, d is at the point K + iK' and n is at point iK' on the imaginary axis. The Jacobian elliptic functions are then the unique doubly periodic, meromorphic functions satisfying the following three properties: Pendulum (mathematics) A so-called "simple pendulum" is an idealization of a "real pendulum" but in an isolated system using the following assumptions: The differential equation which represents the motion of a simple pendulum is where is acceleration due to gravity, is the length of the pendulum, and is the angular displacement.
The differential equation given above is not easily solved, and there is no solution that can be written in terms of elementary functions.