

LastQuake, un robot Twitter vertueux et intelligent. Le 12 août 2014, un article du Monde titrait « Près d’un compte Twitter sur 10 est alimenté automatiquement » et attirait l’attention sur une donnée fournie par la firme elle-même : 8,5 % des comptes considérés comme actifs sont en fait alimentés de façon automatique (soit tout de même 23 millions d’utilisateurs).
Et la journaliste de mentionner ce qu’elle considère comme le plus sérieux des bots : @earthquakeBot. Auparavant Diplomatie digitale, dans son post du 13 juin, donnait quant à lui aussi une analyse des robots sur Twitter en les classifiant en 5 catégories (spammeurs, followers, RT, influenceurs et pourvoyeurs) et prenait en exemple un autre robot « vertueux » du domaine de la sismologie : @earthquakesSF (qui tweete tous les séismes de la région de San Francisco).
Il est vrai que les tremblements de terre sont une illustration de choix de l’idée qu’on se fait d’un robot vertueux car il œuvre sur le délicat sujet des catastrophes naturelles. Modélisation et biologie, récit d'une collaboration à succès. Publication Christophe Godin et Teva Vernoux - © Inria Christophe Godin, de l'équipe Inria Virtual Plants, et Teva Vernoux, du Laboratoire de reproduction et développement des plantes (CNRS/ENS Lyon/INRA/UCBL) ont mené un projet dont les résultats jettent une lumière nouvelle sur la façon dont les plantes forment ces étonnants et universels arrangements d’organes en spirales ou en couronnes. Prendre la mesure du monde. Séismes et tsunamis - Science Actualités (avant 2010) Tsunami : reconstruire la vague. Le tsunami du 26 décembre 2004 a été l’un des plus meurtriers de tous les temps.
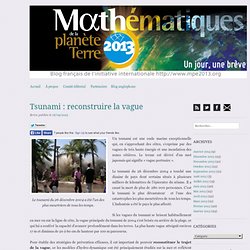
Un tsunami est une onde marine exceptionnelle qui, en s’approchant des côtes, s’exprime par des vagues de très haute énergie et une inondation des zones côtières. Le terme est dérivé d’un mot japonais qui signifie « vague portuaire ». Le tsunami du 26 décembre 2004 a touché une dizaine de pays dont certains situés à plusieurs milliers de kilomètres de l’épicentre du séisme. Il a causé la mort de plus de 280 000 personnes. C’est le tsunami le plus dévastateur et l’une des catastrophes les plus meurtrières de tous les temps. Expliquer les tremblements de terre. Secours lors du tremblement de terre de Kobe en 1995. Les tremblements de terre – ou séismes – et leurs répliques font l’objet d’études approfondies dans les pays où ils causent régulièrement des dégâts humains et matériels considérables.
Les scientifiques disposent d’enregistrements de données qui décrivent précisément la nature de chaque événement sismique (tremblement de terre ou réplique d’un tremblement), son foyer, son épicentre et sa magnitude selon la fameuse échelle (logarithmique) proposée par C.H. Richter en 1935. La stratégie de l’araignée. Prédire les inondations. Prévoir les crues, avec quelle (in)certitude ? Des modèles mathématiques sont utilisés afin de prévoir les risques de crues.
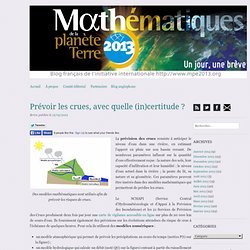
La prévision des crues consiste à anticiper le niveau d’eau dans une rivière, en estimant l’apport en pluie sur son bassin versant. De nombreux paramètres influent sur la quantité d’eau effectivement reçue : la nature des sols, leur capacité d’infiltration et leur humidité ; le niveau d’eau actuel dans la rivière ; la pente du lit, sa nature et sa géométrie. Ces paramètres peuvent être insérés dans des modèles mathématiques qui permettent de prédire les crues. Des équations pour les vagues. Une vague de surf à Maverick en Californie.
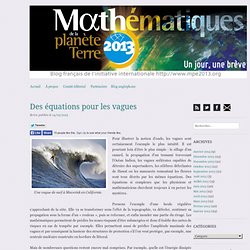
Pour illustrer la notion d’onde, les vagues sont certainement l’exemple le plus intuitif. Il est pourtant loin d’être le plus simple : le sillage d’un canard, la propagation d’un tsunami traversant l’Océan Indien, les vagues scélérates capables de détruire des supertankers, les célèbres déferlantes de Hawaï ou les mascarets remontant les fleuves sont tous décrits par les mêmes équations. Des équations si complexes que les physiciens et mathématiciens cherchent toujours à en percer les mystères. Prenons l’exemple d’une houle régulière s’approchant de la côte. Elle va se transformer sous l’effet de la topographie, va déferler, continuer sa propagation sous la forme d’un « rouleau », puis se reformer, et enfin inonder une partie du rivage.
Mais de nombreuses questions restent encore mal comprises. Le comportement des fourmis renseigne sur la formation des réseaux sociaux. Pour se déplacer, les fourmis appliquent le principe de Fermat ! On sait depuis longtemps que les fourmis savent choisir le chemin le plus court pour accéder à une source de nourriture.
Comment se comportent-elles quand le chemin le plus court n'est pas le plus rapide ? Cette situation se produit par exemple lorsque les fourmis sont obligées de se déplacer sur deux surfaces différentes, où leurs vitesses de déplacement ne sont pas les mêmes. Une récente étude américaine montre que, dans ce cas de figure, les fourmis se comportent de la même manière que la lumière quand elle se propage à travers différents supports : dans les deux cas, l'itinéraire choisi obéit au principe de Fermat et privilégie la rapidité. Les chercheurs ont travaillé sur trois colonies de fourmis, comportant chacune plusieurs milliers d'individus. L'expérience a montré que les fourmis finissaient toujours par se comporter dans leurs déplacements selon le principe de Fermat, c'est-à-dire en empruntant non pas le chemin le plus court mais le plus rapide. Phys.org. Simuler les avalanches.
Avalanche aérosol atteignant la forêt.
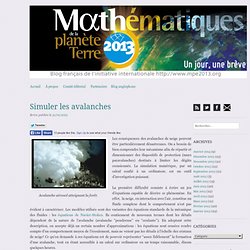
Les conséquences des avalanches de neige peuvent être particulièrement désastreuses. On a besoin de bien comprendre leur mécanisme afin de répartir et dimensionner des dispositifs de protection (murs paravalanches) destinés à limiter les dégâts occasionnés. La simulation numérique, par un calcul confié à un ordinateur, est un outil d’investigation puissant. La première difficulté consiste à écrire un jeu d’équations capable de décrire ce phénomène. En effet, la neige, en interaction avec l’air, constitue un fluide complexe dont le comportement n’est pas évident à caractériser. Toutefois, ces termes supplémentaires qu’on introduit dans des équations “classiques” (mais déjà complexes), en modifient profondément la structure mathématique.
Du jardin au modèle informatique : la phyllotaxie. Comment les feuilles se positionnent-elles sur la tige d’une plante ?
Tout est question de phyllotaxie ! Mais au fait, quel est le lien avec l’informatique et les mathématiques ? Christophe Godin l’explique dans cet épisode du podcast audio. Sur la trace des éléphants de mer. Harem d’éléphants de mer sur les îles Kerguelen.
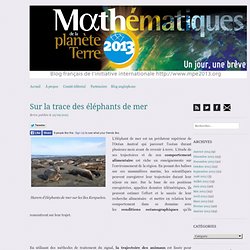
L’éléphant de mer est un prédateur supérieur de l’Océan Austral qui parcourt l’océan durant plusieurs mois avant de revenir à terre. L’étude de ses trajectoires et de son comportement alimentaire est riche en enseignements sur l’environnement de la région. En posant des balises sur ces mammifères marins, les scientifiques peuvent enregistrer leur trajectoire durant leur séjour en mer. Des statistiques pour mettre les systèmes planétaires en équation. Systèmes planétaires Jacky Cresson et Christophe Biernacki, respectivement chercheurs en mathématiques notamment appliquées à l’astronomie et en statistiques dévoileront, d’ici quelques mois, si la répartition des planètes autour de leur étoile suit ou non une loi universelle.
Leurs travaux pourraient aussi révéler l’existence de nouvelles planètes. On sait depuis Galilée (début XVIIe siècle) que Copernic avait vu juste un siècle plus tôt : les planètes gravitent bien autour d’une étoile, le Soleil en l’occurrence dans notre système solaire. Au début du XVIIIe, deux mathématiciens ( Johann Daniel Titius et Johann Elert Bode) mettent cela en équation : ils décrivent la position des planètes connues à cette époque par rapport au Soleil. La loi de Titius-Bode dépend d'une constante et du rang de chaque planète observée par rapport à son étoile. Des mathématiciens dévoilent par hasard l’organisation des galaxies. Astrophysique Mise en évidence des structures filamentaires dans l'organisation des galaxies Les méthodes de reconstruction de formes tridimensionnelles développées par Frédéric Chazal et David Cohen-Steiner, deux chercheurs de l’équipe Geometrica (bilocalisée à Inria Saclay - Île-de-France et Sophia Antipolis-Méditerranée) se révèlent être des outils inespérés pour les astrophysiciens.
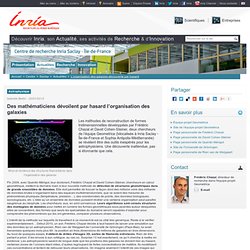
Une découverte inattendue, pas si étonnante que cela. Fin 2009, avec Quentin Mérigot, leur doctorant, Frédéric Chazal et David Cohen-Steiner, chercheurs en calcul géométrique, mettent la dernière main à leur nouvelle méthode de détection de structures géométriques dans de grands ensembles de données. Elle doit permettre de trouver la façon dont des millions voire des milliards de données brutes s’organisent dans des espaces multidimensionnels, que ce soient des mesures de phénomènes physiques (température, pression…), des coordonnées de points, des données biologiques, sociologiques, etc.