

Notes de cours : Triangles isométriques et figures équivalentes. Notes de cours : Les triangles semblables et les relations métriques.
ÉNONCÉS MATHÉMATIQUES. Mes notes. Les figures semblables, isométriques et équivalentes. Lorsque l'on compare deux figures géométriques ensemble, il arrive que l'on remarque des éléments particuliers.
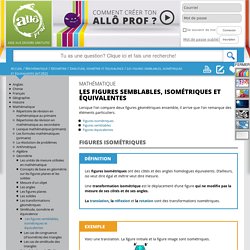
Figures isométriques Les figures isométriques ont des côtés et des angles homologues équivalents. D’ailleurs, iso veut dire égal et métrie veut dire mesure. Une transformation isométrique est le déplacement d’une figure qui ne modifie pas la mesure de ses côtés et de ses angles. La translation, la réflexion et la rotation sont des transformations isométriques. Voici une translation. Un dallage est une figure formée par la superposition de figures isométriques. Figures semblables Des figures semblables sont des figures qui ont exactement la même forme.
Les angles homologues sont congrus, mais les côtés correspondants n’ont pas nécessairement la même mesure. La translation, la rotation et la réflexion entraînent des figures semblables de mêmes dimensions ET isométriques. Voici une homothétie qui a rapetissé le triangle. Figures équivalentes Un trapèze possède une aire de 30 cm². Les cas de congruence (d'isométrie) des triangles. Quand deux triangles sont identiques (mêmes côtés et mêmes angles), on dit qu’ils sont congrus (ou isométriques).
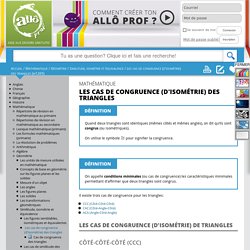
On utilise le symbole pour signifier la congruence. On appelle conditions minimales (ou cas de congruence) les caractéristiques minimales permettant d'affirmer que deux triangles sont congrus. Il existe trois cas de congruence pour les triangles: Les cas de similitude des triangles. Deux triangles qui ont les mêmes angles et des rapports de côtés homologues proportionnels sont dits semblables.
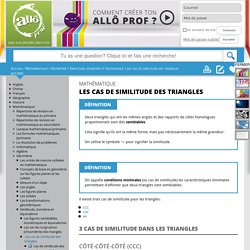
Cela signifie qu'ils ont la même forme, mais pas nécessairement la même grandeur. On utilise le symbole pour signifier la similitude. On appelle conditions minimales (ou cas de similitude) les caractéristiques minimales permettant d'affirmer que deux triangles sont semblables. Il existe trois cas de similitude pour les triangles: Côté-côté-côté (CCC) Lorsque les rapports des 3 côtés homologues des triangles sont égaux, ces triangles sont semblables. Puisque les rapports des côtés homologues sont égaux (tous égaux à 2) Les deux triangles sont semblables par C-C-C. Côté-angle-côté (CAC) Deux triangles sont semblables lorsqu’un angle congru est compris entre deux côtés homologues proportionnels. L'angle congru (90°) se trouve entre 2 côtés dont les rapports sont égaux (les rapports égalent 2) Les deux triangles sont semblables par C-A-C.
Angle-angle (AA) Cas CCC Cas CAC Cas AA. Les relations métriques dans le triangle rectangle. La hauteur issue de l'angle droit dans un triangle rectangle ABC détermine deux autres triangles rectangles, les triangles ACD et BCD.
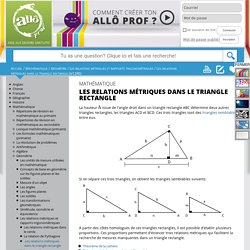
Ces trois triangles sont des triangles semblables entre eux. Si on sépare ces trois triangles, on obtient les triangles semblables suivants: À partir des côtés homologues de ces triangles rectangles, il est possible d'établir plusieurs proportions. Ces proportions permettent d'énoncer trois relations métriques qui facilitent la recherche de mesures manquantes dans un triangle rectangle. Théorème de la cathète Dans un triangle rectangle, la mesure de chaque côté de l’angle droit est la moyenne proportionnelle entre la mesure de sa projection sur l’hypoténuse et celle de l’hypoténuse entière.
Puisque les triangles ABC, ADB et BDC sont semblables, on peut déterminer la relation métrique suivante: 1) ou 2) ou Déterminer la mesure de dans le triangle suivant: Selon la relation , on peut dire que: La mesure du côté est de 8 cm. Relations métriques (Résumé) Formules de périmètre, aire et volume. Mathématique Formules de périmètre - Pour calculer le périmètre d’une figure plane, il suffit d’additionner la mesure de tous ses côtés.
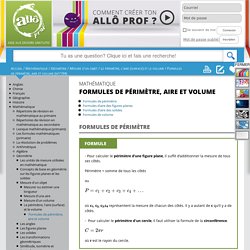
Périmètre = somme de tous les côtés ou où c1, c2, c3,c4 représentent la mesure de chacun des côtés. . - Pour calculer le périmètre d'un cercle, il faut utiliser la formule de la circonférence. où r est le rayon du cercle. Calculer le périmètre des figures suivantes: Périmètre = somme de tous les côtésPérimètre = 3 cm + 6 cm + 10 cm + 6 cmPérimètre = 25 cm Périmètre = somme de tous les côtés Périmètre = 6 cm + 6 cm + 6 cm + 6 cm Périmètre = 24 cm Formules d'aire des figures planes Formules d'aire des solides Formules de volume.