

Associative array. Pairs, such that each possible key appears at most once in the collection.
Operations associated with this data type allow:[1][2] Hash table. A small phone book as a hash table Hashing[edit]
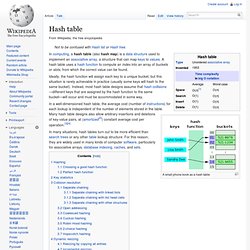
Hash function. A hash function that maps names to integers from 0 to 15.
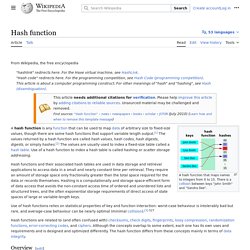
There is a collision between keys "John Smith" and "Sandra Dee". Uses[edit] Hash tables[edit] Thus, the hash function only hints at the record's location. Still, in a half-full table, a good hash function will typically narrow the search down to only one or two entries. People who write complete hash table implementations choose a specific hash function—such as a Jenkins hash or Zobrist hashing—and independently choose a hash-table collision resolution scheme—such as coalesced hashing, cuckoo hashing, or hopscotch hashing. Caches[edit] Bloom filters[edit] Finding duplicate records[edit] Bloom filter. Bloom proposed the technique for applications where the amount of source data would require an impracticably large hash area in memory if "conventional" error-free hashing techniques were applied.
He gave the example of a hyphenation algorithm for a dictionary of 500,000 words, out of which 90% follow simple hyphenation rules, but the remaining 10% require expensive disk accesses to retrieve specific hyphenation patterns. With sufficient core memory, an error-free hash could be used to eliminate all unnecessary disk accesses; on the other hand, with limited core memory, Bloom's technique uses a smaller hash area but still eliminates most unnecessary accesses. Priority queue. Operations[edit] A priority queue must at least support the following operations: More advanced implementations may support more complicated operations, such as pull_lowest_priority_element, inspecting the first few highest- or lowest-priority elements, clearing the queue, clearing subsets of the queue, performing a batch insert, merging two or more queues into one, incrementing priority of any element, etc.
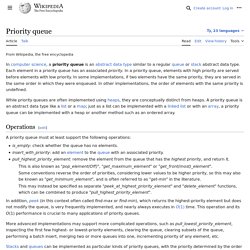
Similarity to queues[edit] Stacks and queues may be modeled as particular kinds of priority queues. Heap. Example of a complete binary max-heap with node keys being integers from 1 to 100 1. the min-heap property: the value of each node is greater than or equal to the value of its parent, with the minimum-value element at the root. 2. the max-heap property: the value of each node is less than or equal to the value of its parent, with the maximum-value element at the root.
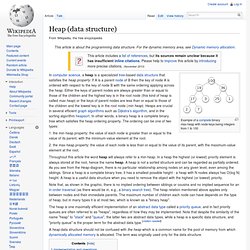
Throughout this article the word heap will always refer to a min-heap. In a heap the highest (or lowest) priority element is always stored at the root, hence the name heap. A heap is not a sorted structure and can be regarded as partially ordered. Note that, as shown in the graphic, there is no implied ordering between siblings or cousins and no implied sequence for an in-order traversal (as there would be in, e.g., a binary search tree). Binary heap. Example of a complete binary max heap Example of a complete binary min heap Shape property A binary heap is a complete binary tree; that is, all levels of the tree, except possibly the last one (deepest) are fully filled, and, if the last level of the tree is not complete, the nodes of that level are filled from left to right.
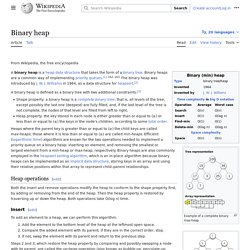
Heap property Heaps with a mathematical "greater than or equal to" (≥) comparison predicate are called max-heaps; those with a mathematical "less than or equal to" (≤) comparison predicate are called min-heaps. Binary tree. Not to be confused with B-tree.
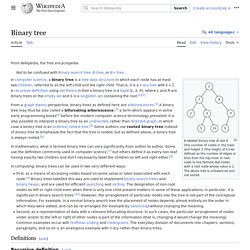
Binary search tree. A binary search tree of size 9 and depth 3, with 8 at the root.
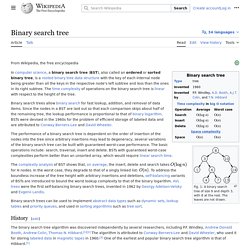
The leaves are not drawn. Binary search trees keep their keys in sorted order, so that lookup and other operations can use the principle of binary search: when looking for a key in a tree (or a place to insert a new key), they traverse the tree from root to leaf, making comparisons to keys stored in the nodes of the tree and deciding, on the basis of the comparison, to continue searching in the left or right subtrees. On average, this means that each comparison allows the operations to skip about half of the tree, so that each lookup, insertion or deletion takes time proportional to the logarithm of the number of items stored in the tree. This is much better than the linear time required to find items by key in an (unsorted) array, but slower than the corresponding operations on hash tables. Self-balancing binary search tree.
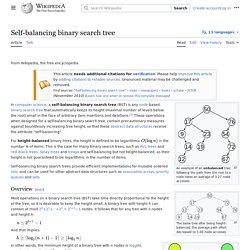
An example of an unbalanced tree; following the path from the root to a node takes an average of 3.27 node accesses The same tree after being height-balanced; the average path effort decreased to 3.00 node accesses.
Red–black tree. A red–black tree is a data structure which is a type of self-balancing binary search tree. Balance is preserved by painting each node of the tree with one of two colors (typically called 'red' and 'black') in a way that satisfies certain properties, which collectively constrain how unbalanced the tree can become in the worst case. Queue (abstract data type) Queues are common in computer programs, where they are implemented as data structures coupled with access routines, as an abstract data structure or in object-oriented languages as classes. Common implementations are circular buffers and linked lists. Theoretically, one characteristic of a queue is that it does not have a specific capacity. Regardless of how many elements are already contained, a new element can always be added.
It can also be empty, at which point removing an element will be impossible until a new element has been added again. Linked list. A linked list whose nodes contain two fields: an integer value and a link to the next node. The last node is linked to a terminator used to signify the end of the list. The principal benefit of a linked list over a conventional array is that the list elements can easily be inserted or removed without reallocation or reorganization of the entire structure because the data items need not be stored contiguously in memory or on disk, while an array has to be declared in the source code, before compiling and running the program.
Linked lists allow insertion and removal of nodes at any point in the list, and can do so with a constant number of operations if the link previous to the link being added or removed is maintained during list traversal. On the other hand, simple linked lists by themselves do not allow random access to the data, or any form of efficient indexing. Double-ended queue. Naming conventions[edit] Distinctions and sub-types[edit] An input-restricted deque is one where deletion can be made from both ends, but insertion can be made at one end only.An output-restricted deque is one where insertion can be made at both ends, but deletion can be made from one end only. Operations[edit] Names vary between languages; major implementations include: Stack (abstract data type) Similar to a stack of plates, adding or removing is only possible at the top.
Simple representation of a stack runtime with push and pop operations. push, which adds an element to the collection, andpop, which removes the most recently added element that was not yet removed. Skip list. In computer science, a skip list is a data structure that allows fast search within an ordered sequence of elements. Fast search is made possible by maintaining a linked hierarchy of subsequences, each skipping over fewer elements. Searching starts in the sparsest subsequence until two consecutive elements have been found, one smaller and one larger than or equal to the element searched for.
Dynamic array. Several values are inserted at the end of a dynamic array using geometric expansion. Grey cells indicate space reserved for expansion. Most insertions are fast (constant time), while some are slow due to the need for reallocation (Θ(n) time, labelled with turtles). Disjoint-set data structure. MakeSet creates 8 singletons. After some operations of Union, some sets are grouped together. Find: Determine which subset a particular element is in. This can be used for determining if two elements are in the same subset.Union: Join two subsets into a single subset.
In order to define these operations more precisely, some way of representing the sets is needed. One common approach is to select a fixed element of each set, called its representative, to represent the set as a whole. Locality of reference. In computer science, locality of reference, also known as the principle of locality, is a phenomenon describing the same value, or related storage locations, being frequently accessed. There are two basic types of reference locality – temporal and spatial locality.
Temporal locality refers to the reuse of specific data, and/or resources, within a relatively small time duration. Spatial locality refers to the use of data elements within relatively close storage locations. CPU cache. Overview[edit]