

¿Por qué sólo cuatro colores? - Naukas. Hace algún tiempo os contaba en este mismo blog mi primera actuación como mamá matemática en la clase del mayor de mis hijos, cuando éste tenía 3 años.
Pues bien, tras el éxito obtenido con el diagrama de Voronoi y su indiscutible utilidad para el reparto justo de caramelos, me crecí y desde entonces he seguido visitando,cada vez que puedo y me invitan, las clases de mis dos hijos, para hacer shows matemáticos. En esta gira artística, hace unos meses, otra vez en la clase del mayor, 5º de primaria, (cómo pasa el tiempo…), presenté el Teorema de los cuatro colores, esta vez con la ayuda de Mati, nuestro pequeño proyecto de divulgación para niños. Para esta ocasión el planteamiento fue el siguiente: Como siempre, la curiosidad de los niños no tardó en aparecer y uno ellos preguntó: “Y si sólo tiene 3 provincias, ¿cómo vas a usar los 4 colores?”
Ésa era fácil. La siguiente pregunta no tardó en ser planteada: “ Y España, ¿necesita los 4 colores?” Ea, pues ya lo tenemos. Vamos a ello. Cada uno en su región y Voronoi en la de todos. Estudié matemáticas, sí, por lo de la belleza suprema, ya saben, a cada uno le da por algo.

Pues bien, todo son risas y geometría computacional hasta que la profesora de tu vástago te pide que vayas a clase a contarle a los niños de 3 años a qué te dedicas. Claro que existe la opción de decirles que eres profesora, como su ‘seño’ y que enseñas cosas de los números y de los triángulos, cuadrados y círculos. Pero no es eso lo que hago, ¡eso es mucho más difícil!. Así que, entendiendo que los niños tienen muy clara la proporción directa entre proximidad y pertenencia, me lié la manta a la cabeza y decidí hablarles sobre Diagramas de Voronoi (contando con la experta e inestimable colaboración del padre de la criatura, mi santo, matemático también). ¿Qué es un diagrama de Voronoi? Lo que se dice dividir el espacio en tantas regiones como puntos u objetos tengamos de tal forma qu ea cada punto le asignemos la región formada por todo lo que está más cerca de él que de nadie. Era mi momento.
Dame 4 colores y pintaré el mundo. Clara Grima Ruíz y Raquel Garcia Ulldemolins | 9 julio 2011 —Pues vaya.

—¿Qué te pasa, Ven? —le preguntó su padre. —Que con sólo 4 colores… no puedo colorear los árboles, no hay marrón —contestó el pequeño enfadado. Él y Sal acababan de recibir sus notas en el colegio y como premio a su esfuerzo, sus padres les invitaron a su restaurante italiano favorito. —Mezcla el rojo con el verde, Ven —le aconsejó Sal a su hermano. —Pues pinta el tronco en azul, como si fuera un Picasso de la época azul —intervino Mamá con un guiño —¡Mamá! —Pero bueno, ¿qué le pasa a mi futbolista favorito? Mati se sentó en la mesa, entre los dos hermanitos y se volvió hacia el pequeño: —¿Quieres que te cuente una historia sobre 4 colores?
Mati entregó a cada niño un mapa de España sin colorear. —Tenéis que colorear cada provincia de un color, pero, ¡ojo! Ven y Sal se pusieron cada uno manos a la obra en su mapa, Mati y los papás charlaban sobre cosas de mayores. —¿Por qué? —No se tocan. Construcción de poliedros. Técnicas sencillas: Origami modular. Construcción de poliedros.
Técnicas sencillas Origami modular Origami es lo mismo que papiroflexia. Papiroflexia u origami modular es una técnica que consiste en plegar con papel varios módulos o unidades que, al unirlas (sin pegamento) formarán una figura compleja. En internet hay muchísimos información sobre muchos modelos, en particular, se puede empezar por Origami Resource Center.
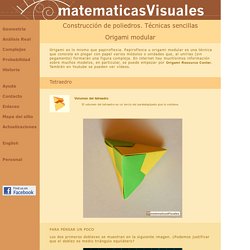
Tetraedro Los dos primeros dobleces se muestran en la siguiente imagen. Podemos construir este tetraedro con dos módulos: Estos son los pasos para construir el tetraedro. Octaedro y tetraedro Una figura sencilla e instructiva está formada por los tres cuadrados en planos ortogonales dos a dos que contienen las 8 aristas del octaedro regular. El dual del tetraedro es otro tetraedro. Geometría. Modelo de papel de un cuboctaedro truncado. Cuboctaedro truncado (.PDF) Imprimir la imagen de abajo (GIF) o el PDF-archivo.
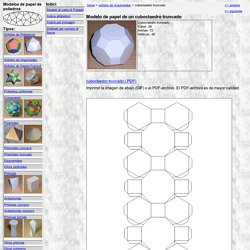
El PDF-archivo es de mayor calidad. Modelo de papelcuboctaedro truncado en colorMedios cuboctaedro truncado LinksVirtual Cuboctaedro Truncado (VRML-viewer es necesario) Copyright el ©1998-2014 Gijs Korthals Altes. Todos los derechos reservados. Geometría modular. Construcción de poliedros.