

La suite de Fibonacci. Le nombre d'or. Fruits d'Eucalyptus provenant de Galice en Espagne.

On trouve des pentagones réguliers, mais aussi des carrés er des triangles équilatéraux. Lien avec l'ensoleillement Cela vient de ce que l'ensoleillement doit être maximum pour toutes les feuilles et on démontre que l'angle de deux feuilles consécutives doit être voisin d'un certain k ème de tour ; les fractions de Fibonacci sont les fractions les plus voisines de k. Les graines dans une fleur de tournesol Ammonite L'enroulement régulier d'une ammonite se fait suivant une spirale logarithmique. Suite de Fibonacci dans la nature. Loi Les bourgeons tenteraient de disposer du maximum de lumière et de place.

Le premier se place. Le nombre d'or - Micmaths. Leonardo Fibonacci. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges De son vrai nom Léonard de Pise, dit Fibonacci (signifiant "fils de Bonaccio"), Leonardo est le fils d'un administrateur de la ville de Pise.

Commerçant et grand voyageur, il parcourut l'Europe et les pays d'orient tout en s'imprégnant des mathématiques de son époque inspirées des mondes grecs, indiens et arabes. Dans son Liber Abaci (Livre de calcul), publié en 1202, principalement consacré aux calculs commerciaux, il affine et résout des problèmes algébriques déjà rencontrés dans l'œuvre du mathématicien Al Khwarizmi. Fibonacci fait grand usage des nombres dits "arabes" (système décimal positionnel), du calcul fractionnaire ( The fabulous Fibonacci flower formula. Music From The Fibonacci Sequence. DM nb d'or 2nd degré. Collection de nombres, nombre d'or, divine proportion,section dorée. Nombre d'or - ce qu'il faut savoir en bref. Étapes de construction 1) Je construis un carré ABCD de 10 carreaux de côté. 2) Je positionne le point milieu M, en bas. 3) Je dessine un cercle de centre M et de rayon MB; il coupe la droite DC en F. 4) Le rectangle ABEF est un rectangle d'or.

Mesures et conclusions Je mesure le grand côté DF: 16,2 carreaux Le rapport (ou le quotient) entre les mesures de la longueur et de la largueur est Si je calcule le rapport pour le rectangle BEFC, je trouve Soit, à peu près la même valeur. Ce nouveau rectangle BEFC est aussi un rectangle d'or. Valeur exacte du nombre d'or Le triangle BCM est rectangle, je peux lui appliquer le théorème de Pythagore: Cette valeur confirme les mesures effectuées sur les deux rectangles. Calcul des termes de la suite de Fibonacci en ligne. Rechercher un outil (en entrant un mot clé):
Le Nombre d'Or - Chronique Spéciale. Nature by Numbers. Images des mathématiques. Le 2 septembre 2019 - Ecrit par Fernando Corbalán Cet article a été écrit en partenariat avec L’Institut Henri Poincaré Lire l'article en En 2013, l’Institut Henri Poincaré et Images des Mathématiques ont uni leurs efforts pour superviser la réédition de la collection Le monde est mathématique, publiée par RBA en partenariat avec Le Monde.
En 40 ouvrages, cette collection de qualité, issue d’un projet collectif de mathématiciens espagnols, vise à présenter, à travers une grande variété de points de vue, de multiples facettes des sciences mathématiques, sous un aspect historique, humain, social, technique, culturel ... Reprise et améliorée au niveau de la forme, cette édition a été entièrement lue et corrigée par l’équipe d’Images des Mathématiques ; des préfaces et listes bibliographiques ont été ajoutées. En 2019, cette collection est de nouveau éditée, présentée par Étienne Ghys et distribuée par L’Obs. Extrait du Chapitre 1 Un monde doré. Le nombre d'or. (Vitruve, architecte romain 1er siècle avant notre ère). Ainsi si a et b sont les deux grandeurs alors nous aurons : a/b = (a + b) / a. A/b = 1 + b/a pour simplifier, prenons comme variable x = a/b. alors nous obtenons : x = 1 + 1/x x - 1 - 1/x = 0 comme x non nul, nous obtenons l'équation suivante que nous noterons (E) : x2 - x - 1 = 0 qui admet comme racine positive : x = que nous notons Φ et vaut à peu près 1,618...
C'est cette valeur qui est appelée le nombre d'or (dit Φ (phi) en hommage au sculpteur grec Phidias qui s'en servit dans les proportions du Parthénon à Athènes. En espagne, deux tableaux de Antonio de Garcia de Pablo, muchas gracias ;): Pour voir les images suivantes en plus grand les cliquer A ce stade, je vous soumets un petit problème que m'a proposé Dominique Payeur : Je dispose d'un capital. Nous pouvons d'ores et déjà noter quelques résultats : On pourrait aussi sans équation du second degré montrer que 1/Φ = Φ - 1. Le nombre d'or. L' histoire ...

Il y a 10 000 ans : Première manifestation humaine de la connaissance du nombre d'or (temple d'Andros découvert sous la mer des Bahamas). 2800 av JC : La pyramide de Khéops a des dimensions qui mettent en évidence l'importance que son architecte attachait au nombre d'or. Vè siècle avant J-C. (447-432 av.JC) : Le sculpteur grec Phidias utilise le nombre d'or pour décorer le Parthénon à Athènes, en particulier pour sculpter la statue d'Athéna Parthénos . Il utilise également la racine carrée de 5 comme rapport.
IIIè siècle avant J-C. : Euclide évoque le partage d'un segment en "extrême et moyenne raison" dans le livre VI des Eléments. 1498 : Fra Luca Pacioli, un moine professeur de mathématiques, écrit De divina proportione ("La divine proportion"). Au cours du XXème siècle : des peintres tels Dali et Picasso, ainsi que des architectes comme Le Corbusier, eurent recours au nombre d'or. Dossier - La suite de Fibonacci et le nombre d'or - Podcast Science. Disclaimer : Ouh-la, cet article du tout début de notre site est un peu étrange !
On s’était apparement laissé un peu avoir par la nombre-d’or-mania et, avec quelques années de recul, on est pas extrêmement fier de son contenu. On vous propose donc plutôt d’aller voir ce billet de l’excellent blog Choux romanesco, Vache qui rit et intégrales curvilignes intitulé Le plus doré de tous les nombres qui en parle bien mieux que nous le faisons ici. L’équipe de Podcast Science Dossier de Mathieu dans l’épisode #28.
La suite de Fibonacci doit son nom au mathématicien italien Leonardo Fibonacci qui a vécut au XIIème et XIIIème siècle. Mais il est aussi connu pour avoir mis en évidence une suite mathématique qui porte désormais son nom. Arithm'Antique n°6 - Le nombre d'or. The fabulous Fibonacci flower formula. Arthur Benjamin: La suite magique de Fibonacci. Fibonacci Mystery - Numberphile. Random Fibonacci Numbers - Numberphile. Suite de Fibonacci. La suite est définie par et pour n > 1. Fibonacci. Léonard de Pise dit Fibonacci - Italien (1170 ; 1250) Mathématicien italien né à Pise, Léonardo Bonacci a vécu à l’époque de la construction de la célèbre tour penchée.
Il doit son surnom de « Fibonacci », contraction du latin « filius Bonaccii » à son père, marchand de la ville de Pise (grand lieu de commerce en Italie). Très jeune, il accompagne son père en Algérie dans la colonie de Bougie (Bujania) pour être initié à l’arithmétique utile à un futur marchand. Mais son destin en voudra autrement et sera lié à celui de toutes les mathématiques occidentales à venir. A cette époque, l’Italie utilise encore les chiffres romains.
Ses voyages s’étendent par la suite sur toute la méditerranée, en Syrie, en Grèce, en Egypte... Images des mathématiques. La suite de Fibonacci La suite de Fibonacci — bien connue de ceux qui la connaissent bien, comme dirait un célèbre collègue New-Yorkais — commence ainsi : Ses deux premiers termes sont et , et ensuite, chaque terme successif est la somme des deux termes précédents.
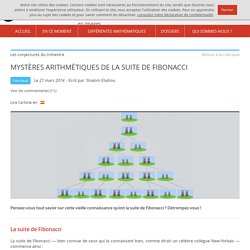
Ainsi , , , , , etc. Comme c’est la coutume, nous dénoterons par le -ème terme de cette suite, en commençant par . Collection de nombres, Fibonacci, Carroll, lapin. La spirale de Fibonacci. Introduction Leonardo Fibonacci, marchand, comptable, mathématicien italien du XIIIe siècle, est connu pour sa suite de Fibonacci dont les termes sont appelés nombres de Fibonacci.