

La vie de Thalès. Thales: Biography of a Great Thinker. Le théorème de Thalès - Micmaths. Thalès - biographie. Il ramène des connaissances de Babylone: - en particulier: l'astronomie - et se taille une jolie réputation en rentrant au pays.

Il prédit l'éclipse du 28 mai de l'an -585. - Hérodote raconte qu'elle survint au cours d'une bataille. - Elle a pour effet de stopper les combats. - Et d'installer la paix pour longtemps. Thalès n'a certainement pas pu prévoir l'éclipse par calcul des mouvements des astres. Il fait de longs séjours en Égypte. - Lesquels savent construire des pyramides (depuis déjà 1500 ans). - Thalès les bluffent en donnant la hauteur de la grande pyramide. - Il utilise les propriétés des triangles semblables. - qui deviendra le théorème de Thalès (nom donné au 18e siècle). Il est célèbre en Égypte et en Grèce. - Il fait partie des Sept Sages désignés par ses contemporains.
Il fonde la géométrie. Thalès. Théorème de Thalès. Par exemple, à propos des « triangles déterminés par deux droites parallèles coupant deux sécantes », l'étude d'un cas particulier de « l'égalité des rapports » (valeur ) repose sur une telle démarche.
On a coupé un des côtés d'un triangle ABC en trois segments de même longueur : AI = IK = KB. Par I et K, on a mené les parallèles au côté [BC], qui coupent [AC] en J et L respectivement. À l'aide des résultats sur les milieux de deux côtés d'un triangle, on souhaite établir que le côté [AC] se trouve lui aussi coupé en trois régulièrement : AJ = JL = LC. On pourra remarquer que contrairement aux deux cas évoqués pour la classe de 5e, l'évidence « visuelle » du résultat ne fait ici guère de doute ; la question qui se pose est donc celle de l'établir au moyen des résultats déjà acquis.
La première des deux égalités ci-dessus est simple à établir, dès que l'on a remarqué que I est le milieu de [AK]. Théorème de Thalès. Configuration possible du théorème de Thalès : les droites (BC) et (DE) sont parallèles donc les triangles ADE et ABC sont semblables et les longueurs AD, DE, EA sont proportionnelles aux longueurs AB, BC et CA.
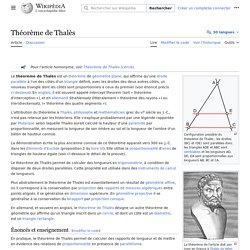
Le théorème de Thalès est un théorème de géométrie qui affirme que, dans un plan, à partir d'un triangle, une droite parallèle à l'un des côtés définit avec les droites des deux autres côtés un nouveau triangle, semblable au premier (voir énoncé précis ci-dessous). En anglais, il est connu sous le nom de intercept theorem (soit « théorème d'interception ») ; en allemand, il est appelé Strahlensatz, c'est-à-dire « théorème des rayons ».
Le théorème de Thalès se généralise en dimension supérieure. Le résultat est équivalent à des résultats de géométrie projective tels que la conservation du birapport par les projections. À un niveau plus élémentaire, le théorème de Thalès sert à calculer des longueurs en trigonométrie, à condition de disposer de deux droites parallèles. . , mais (et et. Biographie de Thalès de Milet. Thalès est le premier mathématicien dont l'histoire ait retenu le nom.
Il est né à Milet (voir une carte), en Asie mineure, sur les côtes méditerranéennes de l'actuelle Turquie, vers 624 av JC. Il convient toutefois d'être prudent avec ces dates, et avec la vie et les découvertes de Thalès. Il ne reste en effet pas d'écrits de Thalès, et s'il est souvent cité dans d'autres textes, il était d'usage à cette époque d'attribuer à des hommes célèbres des découvertes qu'ils n'avaient pas faites. Plus qu'un simple mathématicien, Thalès était un savant universel, curieux de tout, astronome et philosophe, très observateur. Il fut à ce titre un des Sept Sages. Marchand de profession, Thalès entreprit de nombreux voyages en Crête, en Égypte, en Asie.
Mais le fait d'armes de Thalès est sans conteste la prévision d'une éclipse du soleil, probablement celle du 28 mai 585 avant notre ère. Soudain le jour devint nuit. Théorème de Thalès Débutants. Les six étoiles de ce dessin sont toutes semblables Elles sont obtenues à partir de la plus petite en grossissant 2 fois, 3 fois … Je remarque que: les angles des branches des étoiles sont conservés (36°). comparée à l'étoile 1, la branche de l'étoile 3 est trois fois plus grande; et celle de l'étoile 6 est six fois plus grande.
