

What Is The Birthday Paradox? Hashtables, Pigeonholes, and Birthdays. One of the most beloved of all data structures in computer science is the hash table.

A hash table is a data structure that associates keys with values. The primary operation it supports efficiently is a lookup: given a key (e.g. a person's name), find the corresponding value (e.g. that person's telephone number). It works by transforming the key using a hash function into a hash, a number that is used to index into an array to locate the desired location ("bucket") where the values should be. Sun_Jared.pdf. Learn Cryptography — The Birthday Problem. What is the birthday problem?
The birthday problem concerns the probability that, in a set of n random people, some pair of them will have the same birthday. Thanks to something called the pigeonhole principle, probability of two people having the same birthday reaches 100% when n (number of people) reaches 366. However, 99% probability is reached with just 57 people, and 50% probability with only 23 people.
Birthday Paradox. Background Information A graphing-calculator feature that can be used in conjunction with the classic birthday paradox is a random-integer generator.
With the proper commands, this feature allows the calculator to create lists of random birthdays that can serve as data for students to explore. Students can then run calculator-based simulations of the birthday paradox and can explore the fact that more than 50 percent of the time, when groups of "random" strangers are assembled, only twenty-three persons are needed to find a matching pair of birthdays. The prime objective in this activity is to demonstrate the birthday paradox, using it as a springboard into a unit on probability. Lec10.pdf. Bill Nye Demonstration: The Birthday Paradox Tutorial. What 'the birthday paradox' works on? - Tech Entice. A concept used in one-way hash function cryptography attacks, BIND attacks, in roulette, lottery, even estimating DNA sequence collisions or the chances of duplication of your SSN no.

(if you are American that is); the birthday paradox is a phenomenon that deals with the probability of repetition. Traditionally it started with trying to figure out what the chances are of two people having the same birthday (of course excluding twins). Assuming it’s not a leap year and that there is even possibility for each day to be a day of birth; the chances that G-one and Ra-one have the same birthday is 1/365; these two are independent events after all. Now if you ask what’s the probability that 2 out of 3 people under consideration share the same birthday; you are dealing with three combination of matches…3-1,1-2,2-3. Let’s try to model these cases for k people… it gets a bit messy doesn’t it? Case1–deal with 1 guy… no repetition Where n=365 From Taylor’s polynomials: So our equation becomes: Lec10.pdf. Sun_Jared.pdf. Learn Cryptography — The Birthday Problem. Lec10.pdf. Download. Birthday attack. Understanding the problem[edit] , about 7.9%.
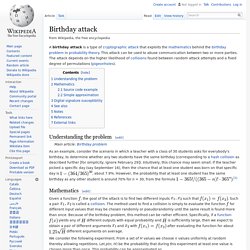
However, the probability that at least one student has the same birthday as any other student is around 70% for n = 30, from the formula Mathematics[edit] Given a function , the goal of the attack is to find two different inputs such that . Yields any of different outputs with equal probability and is sufficiently large, then we expect to obtain a pair of different arguments and with after evaluating the function for about different arguments on average. We consider the following experiment. Let n(p; H) be the smallest number of values we have to choose, such that the probability for finding a collision is at least p. And assigning a 0.5 probability of collision we arrive at. The Birthday Paradox. I have never had a very good relationship with Mathematics.
I used to think it was me… I thought that perhaps I was just a bit put off by Math’s confident demeanor and superior attitude, and by its tendency to micromanage every tiny detail of my universe. But over time I have come to the realization that I’m not the source of the problem. Math, as it turns out, is out of its bloody mind. Consider the following example: Assuming for a moment that birthdays are evenly distributed throughout the year, if you’re sitting in a room with forty people in it, what are the chances that two of those people have the same birthday? For simplicity’s sake, we’ll ignore leap years. The Birthday Paradox. By Katie Bowell, Curator of Cultural Interpretation Today is my birthday.
In this I am far from alone. It turns out that, at least in the Western world, October 5th is the most common day to be born. “What are the odds? ,” you might exclaim. Thinking about how many people in the world share my birthday lead me to think about The Birthday Paradox, and how shared birthdays are more common than you might think. Probability of Repetition: Birthday Paradox Applied to Lotto, Lottery, Roulette. Published in September 2009. • BirthdayParadox.EXE ~ Freeware for a registered member — Permanent Membership.• Collisions.EXE ~ Free probability software for registered members — Permanent (Lifetime) Membership.

This is the most accurate and comprehensive software for calculations in the probability of duplication (or collisions, or coincidences, or repetition), including the tiny Birthday Paradox. The software performs the calculations both ways: 1) Calculate the probability (degree of certainty) when the number of persons (elements) is known; 2) Calculate the number of persons (elements) when the probability is known. The birthday paradox at the World Cup. Image copyright Thinkstock It's puzzling but true that in any group of 23 people there is a 50% chance that two share a birthday.
At the World Cup in Brazil there are 32 squads, each of 23 people... so do they demonstrate the truth of this mathematical axiom? Imagine the scene at the Brazilian football team's hotel. Hulk and Paulinho are relaxing after another stylish win. Math IA final copy. Page days minus 1.
When the third person enters the room, the probability of that person not having the same birthday as the previous two people is simply total number of possible days minus 2. Now simply multiply these numbers to find the probability. As this pattern continues to the 23. Birthday problem. In probability theory, the birthday problem or birthday paradox[1] concerns the probability that, in a set of randomly chosen people, some pair of them will have the same birthday. By the pigeonhole principle, the probability reaches 100% when the number of people reaches 367 (since there are 366 possible birthdays, including February 29).