

Ramanujan–Sato series. In mathematics, a Ramanujan–Sato series[1][2] generalizes Ramanujan’s pi formulas such as, to the form, by using other well-defined sequences of integers obeying a certain recurrence relation, sequences which may be expressed in terms of binomial coefficients , and employing modular forms of higher levels.
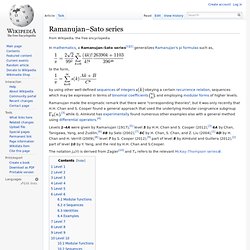
Ramanujan made the enigmatic remark that there were "corresponding theories", but it was only recently that H.H. ,[3] while G. Levels 1–4A were given by Ramanujan (1917),[5] level 5 by H.H. The notation jn(τ) is derived from Zagier[10] and Tn refers to the relevant McKay–Thompson series. Level 1[edit] Examples for levels 1–4 were given by Ramanujan in his 1917 paper. As in the rest of this article. With the j-function j(τ), Eisenstein series E4, and Dedekind eta function η(τ). Which is the smallest degree > 1 of the irreducible representations of the Monster group. Then the two modular functions and sequences are related by, Examples: and Level 2[edit] Then, Level 3[edit] Define, where . And, . J. Eisenstein series. This article describes holomorphic Eisenstein series; for the non-holomorphic case see real analytic Eisenstein series Eisenstein series, named after German mathematician Gotthold Eisenstein, are particular modular forms with infinite series expansions that may be written down directly.
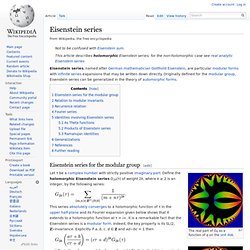
Originally defined for the modular group, Eisenstein series can be generalized in the theory of automorphic forms. Eisenstein series for the modular group[edit] The real part of G6 as a function of q on the unit disk. The imaginary part of G6 as a function of q on the unit disk. Let τ be a complex number with strictly positive imaginary part. This series absolutely converges to a holomorphic function of τ in the upper half-plane and its Fourier expansion given below shows that it extends to a holomorphic function at τ = i∞.
And G2k is therefore a modular form of weight 2k. Relation to modular invariants[edit] Recurrence relation[edit] A directory of all known zeta functions. [This page is under continual construction!

Any contributions would be welcome.] "Over the years striking analogies have been observed between the Riemann zeta-function and other zeta- or L-functions. While these functions are seemingly independent of each other, there is growing evidence that they are all somehow connected in a way that we do not fully understand. In any event, trying to understand, or at least classify, all of the objects which we believe satisfy the Riemann hypothesis is a reasonable thing to do. " J. Abramowitz and Stegun. Page 578. Real analytic Eisenstein series. There are many generalizations associated to more complicated groups.
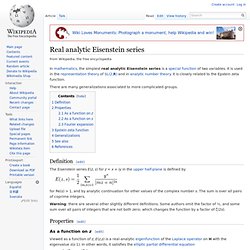
Definition[edit] The Eisenstein series E(z, s) for z = x + iy in the upper half-plane is defined by for Re(s) > 1, and by analytic continuation for other values of the complex number s. Airy zeta function. In mathematics, the Airy zeta function, studied by Crandall (1996), is a function analogous to the Riemann zeta function and related to the zeros of the Airy function.
Definition[edit] The Airy functions Ai and Bi The Airy function. Multiple zeta function. In mathematics, the multiple zeta functions are generalisations of the Riemann zeta function, defined by and converge when Re(s1) + ... + Re(si) > i for all i.
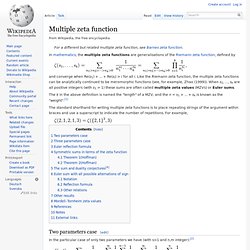
Like the Riemann zeta function, the multiple zeta functions can be analytically continued to be meromorphic functions (see, for example, Zhao (1999)). When s1, ..., sk are all positive integers (with s1 > 1) these sums are often called multiple zeta values (MZVs) or Euler sums. The k in the above definition is named the "length" of a MZV, and the n = s1 + ... + sk is known as the "weight".[1] The standard shorthand for writing multiple zeta functions is to place repeating strings of the argument within braces and use a superscript to indicate the number of repetitions.
Two parameters case[edit] In the particular case of only two parameters we have (with s>1 and n,m integer):[2] where are the generalized harmonic numbers. where Hn are the harmonic numbers. Note that if we have irreducibles, i.e. these MZVs cannot be written as function of. Lerch zeta function. In mathematics, the Lerch zeta-function, sometimes called the Hurwitz–Lerch zeta-function, is a special function that generalizes the Hurwitz zeta-function and the polylogarithm.
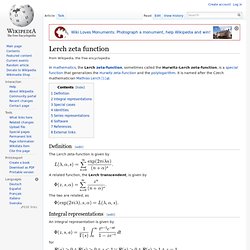
It is named after the Czech mathematician Mathias Lerch [1]. Definition[edit]