

Fotografies · Fotografia Matemàtica. Càlcul del nombre mixt a partir de la fracció impròpia. Nombres mixtos - La vostra aula. MATEMÁTICAS - LA SUPERFICIE. Tema 9: Mesures, unitats de longitut, massa, capacitat i superfície. Unitats de mesura - 6è de primària. Medidas de superficie. Mate, 6º Primaria. La Eduteca - Magnitudes: las unidades de capacidad. La Eduteca - Magnitudes: las unidades de masa. La longitud y su unidad de medida. El metro. Truco de matemáticas para leer la mente. LA PIRAMIDE DE POBLACION. Segle XVI- Sapiens.cat. Ja en el segle XVIII, autors com José Cadalso o Campomanes constataren el creixement econòmic del Principat que diferencià Catalunya de la resta de la península.
Entre els autors espanyols estava canviant l’estereotip del poble català. Així, del tòpic del català bandoler es va passar al tòpic del català treballador i estalviador (“los holandeses de España”). En el propi segle XVIII va sorgir una interpretació històrica per explicar aquest creixement i l’atribuïen als efectes produïts per la monarquia borbònica des de la implantació de la Nova Planta. Aquesta teoria explicativa de l’expansió econòmica catalana tindrà una continuïtat al llarg del temps. Serà amb l’obra de Pierre Vilar, Catalunya dins de l’Espanya Moderna, quan es contradigui la interpretació tradicional per explicar el creixement del segle XVIII en els canvis produïts durant el segle XVII. En aquest període es posa de relleu la recuperació demogràfica i el redreçament econòmic després de la crisi de la Baixa Edat Mitjana.
Sèrie històrica - Àrea metropolitana de Barcelona. Estudiantes – IDM. f47 mosaics amb peces mobils. Dibuix Geomètric. Construcción de polígonos a partir del lado por el método general (endecágono). Construcciones con regla y compás (III): Los polígonos regulares - Gaussianos. Ir a Construcciones con regla y compás (II) Terminamos esta serie dedicada a las construcciones con regla y compás con un artículo sobre la relación de éstas con los polígonos regulares.
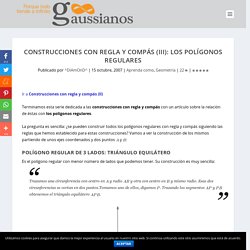
La pregunta es sencilla: ¿se pueden construir todos los polígonos regulares con regla y compás siguiendo las reglas que hemos establecido para estas construcciones? Vamos a ver la construcción de los mismos partiendo de unos ejes coordenados y dos puntos y Polígono regular de 3 lados: Triángulo equilátero Es el polígono regular con menor número de lados que podemos tener. Trazamos una circunferencia con centro en y radio y otra con centro en y mismo radio. Polígono regular de 4 lados: Cuadrado. Construccions de polígons regulars simples per mètodes exactes (resum) Construcció polígons regulars. Mosaics amb polígons regulars. Construcció polígons regulars. Aprenem Matemàtiques: Polígons.
POLÍGON: És la porció del pla limitada per una línia poligonal tancada.

Els seus elements són: Matemàtiques i art. Matemáticas y arte. Maths and art. Els mosaics regulars són aquells que recobreixen el pla sense deixar espais buits fent servir polígons regulars iguals, de manera que coincideixin arestes amb arestes i que a cada vèrtex hi toquen el mateix nombre de polígons.

Quins poligons regulars coneixem? Els triangles equilàters, els quadrats, i també els pentàgons, hexàgons, heptàgons regulars... . . . Però no tots ens serveixen per construir mosaics regulars. Geoplans i pensament exhaustiu. Creiem en la importància de proposar als nostres alumnes recórrer l'itinerari: trobar una solució d'un problema que en té diverses, trobar algunes d'aquestes solucions i finalment, trobar totes les solucions.
Aquest creença ve acompanyada d'una altra: la necessitat de treballar intencionadament aquest itinerari a les classes i de promoure discussions relacionades amb les preguntes:com saps que no hi ha altres solucions? Quina estratègia has seguit per no perdre cap solució? Activitats de pentomino. - España. Matemáticas Amigas. Alexey Pazhitnov. Alexey Pazhitnov -cuyo apellido a veces se ve transliterado como «Pajitnov«- nació en Rusia en 1956.
Su interés por la ciencia y por las matemáticas en particular -aunque también le gustaba la psicología- le llevó a trabajar en el «Computer Centre of the Soviet Academy of Sciences«, un centro de investigación y desarrollo fundado por el gobierno Soviético. En 1985 compra un pentomino, un juego de origen árabe que consiste en rellenar un rectángulo con las 12 piezas distintos sin dejar huecos vacíos ni superponiendo cuadrados. Como cada una de las piezas ocupa 5 cuadros -de ahí lo de «pento»-, el rectángulo resultante tiene un área de 60 cuadrados, siendo posibles los tamaños de 3×20, 4×15, 5×12 y 6×10, teniendo cada uno múltiples soluciones. Para transformar el pentomino en un videojuego interesante, a Alexey y a su colega Dmitry Pavlovsky se les ocurrieron dos mejoras: añadir el factor tiempo -jugar contrarreloj-, y hacerlo más sencillo.
«Pandora’s Box» para Windows en 1999. Gràfics a les Ciències Socials. Quan es vol representar l'estructura de la població per grups d'edats i sexes.

En tot el procés de construcció hem de tenir en compte que és un gràfic doble, una meitat per les dones (la dreta) i l'altra pels homes (l'esquerra). Primer pas: L'eix horitzontal (o d'abcises) es marquen els percentatges. Segon pas: A l'eix vertical o d'ordenades se situen les edats de la població agrupades en cohorts (intervals de 5 anys: de 0 a 4 anys, de 5 a 9,...)