

Möbius strip. A Möbius strip made with a piece of paper and tape.
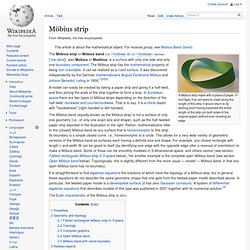
If an ant were to crawl along the length of this strip, it would return to its starting point having traversed the entire length of the strip (on both sides of the original paper) without ever crossing an edge. The Möbius strip or Möbius band (UK /ˈmɜrbiəs/ or US /ˈmoʊbiəs/; German: [ˈmøːbi̯ʊs]), also Mobius or Moebius, is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable.
It can be realized as a ruled surface. It was discovered independently by the German mathematicians August Ferdinand Möbius and Johann Benedict Listing in 1858.[1][2][3] The Möbius band (equally known as the Möbius strip) is not a surface of only one geometry (i.e., of only one exact size and shape), such as the half-twisted paper strip depicted in the illustration to the right. The Euler characteristic of the Möbius strip is zero. Properties[edit] August Ferdinand Möbius Topology[edit] Neighbourhood (mathematics) A set if a small disk around is contained in A rectangle is not a neighbourhood of any of its corners.
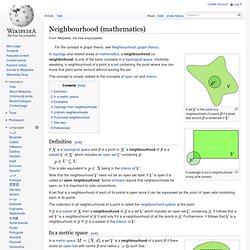
If is a topological space and is a point in , a neighbourhood of is a subset of , which includes an open set containing This is also equivalent to Note that the neighbourhood need not be an open set itself. Is open it is called an open neighbourhood. A set that is a neighbourhood of each of its points is open since it can be expressed as the union of open sets containing each of its points. Sphere Inside out Part - I. Manifold. A manifold is a topological space that is locally Euclidean (i.e., around every point, there is a neighborhood that is topologically the same as the open unit ball in ).
To illustrate this idea, consider the ancient belief that the Earth was flat as contrasted with the modern evidence that it is round. The discrepancy arises essentially from the fact that on the small scales that we see, the Earth does indeed look flat. In general, any object that is nearly "flat" on small scales is a manifold, and so manifolds constitute a generalization of objects we could live on in which we would encounter the round/flat Earth problem, as first codified by Poincaré. More concisely, any object that can be "charted" is a manifold.
One of the goals of topology is to find ways of distinguishing manifolds. As a topological space, a manifold can be compact or noncompact, and connected or disconnected. If a manifold contains its own boundary, it is called, not surprisingly, a "manifold with boundary. " . Manifold Tangent Vector. Roughly speaking, a tangent vector is an infinitesimal displacement at a specific point on a manifold.
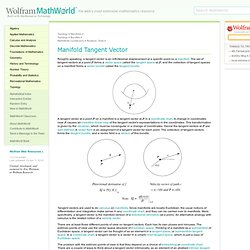
The set of tangent vectors at a point forms a vector space called the tangent space at , and the collection of tangent spaces on a manifold forms a vector bundle called the tangent bundle. A tangent vector at a point on a manifold is a tangent vector at in a coordinate chart. Causes an invertible linear map of the tangent vector's representations in the coordinates. Are well-defined. Tangent vectors are used to do calculus on manifolds. There are at least three different points of view on tangent vectors. The problem with the extrinsic points of view is that they depend on a choice of embedding or coordinate chart. It is important to distinguish tangent vectors at from tangent vectors at any other point , although they may seem parallel.
. , for instance, any smooth vector field must vanish somewhere. Topology.