

Lo sapevate che…Il paradosso di Zenone. Il paradosso di "Achille e la Tartaruga" è il paradosso di Zenone più famoso, proposto nel V sec. a.C. da Zenone di Elea per difendere le tesi del suo maestro Parmenide, che sosteneva che il movimento fosse un'illusione e che la realtà fosse costituita da un Essere unico e immutabile.
Le argomentazioni di Zenone si basano su riduzioni all'assurdo, cioè tendono a confutare un'ipotesi assumendola inizialmente come vera e facendo poi vedere con un ragionamento che da quell'ipotesi segue necessariamente una contraddizione e pertanto deve essere rifiutata. Tale modalità di argomentare è derivata da un metodo di dimostrazione molto comune in matematica: la dimostrazione per assurdo. Di seguito la famosa formulazione dello scrittore argentino Jorge Luis Borges: "Achille, simbolo di rapidità, deve raggiungere la tartaruga, simbolo di lentezza. Edutopia. Quali trucchi vengono spesso usati per far percepire i grafici in maniera favorevole verso ciò che si vuole mostrare? - Quora.
Per prima cosa, al fine di ingannare la percezione visiva, è possibile utilizzare la prospettiva, utilizzando immagini tridimensionali.
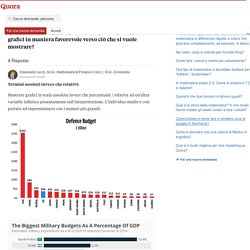
Per questo motivo è sempre sconsigliabile far riferimento a grafici a torta 3D. Per esempio, alla pagina 3D Graphs Fool the Viewer’s Eye è possibile vedere come lo stesso grafico può essere rotato, al fine di manipolare la comprensione del pubblico, pur restando fedeli ai dati. Il grafico ha evidentemente due sezioni identiche, tanti sono i Pros quanti i Cons, ma se lo ruotiamo in questo modo. SinusoideTrasformata. Viewer - Learning Designer. - Watch individually these two resources available at the work space: (1) Atomic testing in Marshall islands: (2) Postcards from Pripyat: Discuss with your group after the videos: 1) Where do video events take place?
Viewer - Learning Designer. Catenaria. La matematica del prof. Francesco Daddi - Journal. Anche-i-ponti-hanno-unequazione. Pizzeide: un’odissea alla scoperta di pizze tonde e quadrate! DesmosTransformationsActivity.docx. Duomo di Firenze, il sole passa dal più grande gnomone del mondo. Contenuto Articolo Si trova nel Duomo di Firenze il più grande gnomone del mondo.
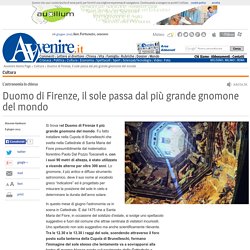
Fu fatto installare nella Cupola di Brunelleschi che svetta nella Cattedrale di Santa Maria del Fiore presumibilmente dal matematico fiorentino Paolo Dal Pozzo Toscanelli e, con i suoi 90 metri di altezza, è stato utilizzato a vicende alterne per oltre 300 anni. Lo gnomone, il più antico e diffuso strumento astronomico, deve il suo nome al vocabolo greco “indicatore” ed è progettato per misurare la posizione del sole in cielo e determinare la durata dell’anno solare. In questo mese di giugno l'astronomia va in scena in Cattedrale. È dal 1475 che a Santa Maria del Fiore, in occasione del solstizio d'estate, si svolge uno spettacolo suggestivo e fuori dal comune che attrae centinaia di visitatori incuriositi.
Il fenomeno è visibile al pubblico nei giorni 8, 12, 20 e 25 giugno, dalle ore 12.30 alle 13.30, nella cappella della Croce, a sinistra dell’altare maggiore. Population Growth. Getting the Picture: Communicating Data Visually According to U.S. census estimates, the population of Texas grew from 17,045,000 people in 1990 to 18,378,000 in 1994.
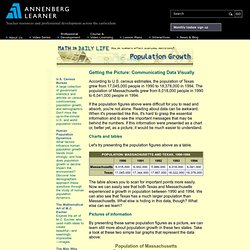
The population of Massachusetts grew from 6,018,000 people in 1990 to 6,041,000 people in 1994. If the population figures above were difficult for you to read and absorb, you're not alone. Reading about data can be awkward. Smaltimento farmaci dal corpo: modello matematico. Overthinking my teaching. Definition: The quotient, factor a, of c is b if and only if ab is c.
We introduce the following notation: Examples When we read this notation aloud, we say (for the second example), The quotient, factor 5, of 10 is 2. The important thing to remember about a quotient is that a quotient is a factor. When we see this equation: we ask ourselves, What factor goes with 3 to make 12? Three Claims Function Carnival Makes About Online Math Education. Today Desmos is releasing Function Carnival, an online math happytime we spent several months developing in collaboration with Christopher Danielson.
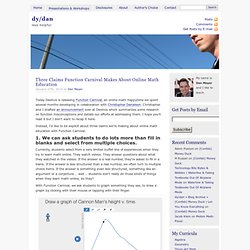
Christopher and I drafted an announcement over at Desmos which summarizes some research on function misconceptions and details our efforts at addressing them. I hope you'll read it but I don't want to recap it here. Instead, I'd like to be explicit about three claims we're making about online math education with Function Carnival. Visualpatterns. Graphing Stories - 15 seconds at a time. I logaritmi. Mi sono informato.
Oggi i programmi scolastici dei licei scientifici parlano di logaritmi ma intendono quelli “naturali”, quelli cioè che appaiono naturalmente in analisi matematica. Sono ormai scomparse le tavole logaritmiche, quel libriccino che almeno ai miei tempi veniva sfruttato soprattutto per nascondere al suo interno le formule di trigonometria alla maturità e nessuno sapeva usare bene. Oggettivamente le tavole logaritmiche sono ormai inutili, quando una calcolatrice da dieci euro ha il tasto “log” che dà subito il risultato; e comunque la calcolatrice assolve allo stesso compito per cui i logaritmi “volgari” erano nati. Trasmissione sulla parabola.mp4. Metodo dello gnomone di cartoncino. Matematicamedie: Teorema dello gnomone [Aggiornato]