

Kawasaki's theorem. In this example, the alternating sum of angles (starting from the triangle in the bottom of the crease pattern) is 90 − 45 + 22.5 − 22.5 + 45 − 90 + 22.5 − 22.5 = 0.
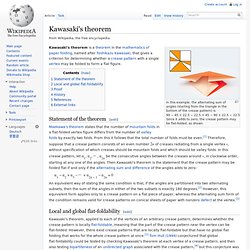
Since it adds to zero, the crease pattern may be flat-folded, as shown. Statement of the theorem[edit] Maekawa's theorem states that the number of mountain folds in a flat-folded vertex figure differs from the number of valley folds by exactly two folds. From this it follows that the total number of folds must be even.[1] Therefore, suppose that a crease pattern consists of an even number 2n of creases radiating from a single vertex v, without specification of which creases should be mountain folds and which should be valley folds. In this crease pattern, let α1, α2, ⋯, α2n be the consecutive angles between the creases around v, in clockwise order, starting at any one of the angles. α1 − α2 + α3 − ⋯ + α2n − 1 − α2n = 0 Local and global flat-foldability[edit] Proof[edit] α1 − α2 + α3 − ⋯ + α2i − 1 − α2i History[edit]
Kawasaki's Theorem. The Theorems of Maekawa, Kawasaki, and Justin. Lecture 20 in 6.849: Geometric Folding Algorithms: Linkages, Origami, Polyhedra (Fall 2010) Lecture 3 in 6.849: Geometric Folding Algorithms: Linkages, Origami, Polyhedra (Fall 2010) Figure 16.2 from GFALOP.
BOS academic : The Miura-Ori map. The Miura-Ori map by Ian Bain Folded maps are merciless to the user who makes the slightest error in returning them to their compact form.

Pt the Tokyo ICA meeting Koryo Miura and Masamori Sakamaki from Tokyo University's Institute of Space and Aeronautical Science demonstrated an application, of space science, combined with a little Origami, which transforms the ergonomics of map folding. Miura and Sakamaki normally work on the problems of packing large flat items, like satellite antennae and solar collectors, into the smallest, most compact shapes with a view to deploying them as rapidly and as simply as possible. They saw three problems with naps folded at right angles in the conventional manner. The key to an alternative system of may folding lies in the ancient Japanese art of paper-folding, origami. Professor Koryo Miura has since sent us a copy of the paper which was distributed at the International Cartographical Association's conference last August. Other related sites include; Miura Map Fold. The Miura-Ori Map. A warm welcome to you dear reader!
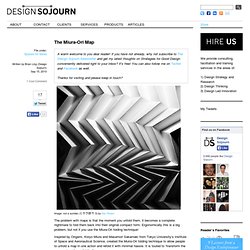
If you have not already, why not subscribe to The Design Sojourn Newsletter and get my latest thoughts on Strategies for Good Design conveniently delivered right to your inbox? It's free! You can also follow me on Twitter and Facebook as well. Thanks for visiting and please keep in touch? Image: not a sunrise (ミウラ折り 3) by Dan Rosen The problem with maps is that the moment you unfold them, it becomes a complete nightmare to fold them back into their original compact form. Inspired by Origami, Koryo Miura and Masamori Sakamaki from Tokyo University’s Institute of Space and Aeronautical Science, created the Muira-Ori folding technique to allow people to unfold a map in one action and refold it with minimal hassle.
Miura and Sakamaki normally work on the problems of packing large flat items, like satellite antennae and solar collectors, into the smallest, most compact shapes with a view to deploying them as rapidly and as simply as possible. Love this post?