

Teorema de Noether. El teorema de Noether es un resultado central en física teórica.
Expresa que cualquier simetría diferenciable, proveniente de un sistema físico, tiene su correspondiente ley de conservación. El teorema se denomina así por la matemática Emmy Noether, quien lo formuló. Además de permitir aplicaciones físicas prácticas, este teorema constituye una explicación de por qué existen leyes de conservación y magnitudes físicas que no cambian a lo largo de la evolución temporal de un sistema físico. Explicación[editar] El teorema de Noether relaciona pares de ideas básicas de la física: (1) una es la invariancia de la forma que una ley física toma con respecto a cualquier transformación (generalizada) que preserve el sistema de coordenadas (aspectos espaciales y temporales tomados en consideración), y la otra es (2) la ley de conservación de una magnitud física. Rotaciones y momento angular[editar] Traslaciones y momento lineal[editar] Invariancia temporal y energía[editar] entonces: . . Son cero y donde. First Conservation Laws Derived For A Virtual Universe.
One of the most important, powerful and beautiful ideas in modern physics is Noether’s theorem.

This essentially says that the fundamental laws of physics are a manifestations of symmetry in the universe. So if the universe has rotational symmetry, then it must also obey the law of conservation of angular momentum, if it has a time symmetry, then energy must be conserved and so on. It’s hard to understate the profound significance of this approach. It seems to tease apart the very fabric of the universe to reveal a very powerful beauty beneath. And yet, peer more closely at Noether’s theorem and you soon find its severe limitations. That specifically excludes discrete systems, which proceed step-by-step. Take for example, Conway’s famous game of life, in which life-like forms can be generated using a cellular automaton.
Clearly Noether’s theorem cannot apply. The system they study is called an Ising spin model. This condition has important consequences. That’s hugely significant. Noether's second theorem. Specifically, the theorem says that if the action has an infinite-dimensional Lie algebra of infinitesimal symmetries parameterized linearly by k arbitrary functions and their derivatives up to order m, then the functional derivatives of L satisfy a system of k differential equations.
See also[edit] Notes[edit] Jump up ^ Noether E (1918), "Invariante Variationsprobleme", Nachr. D. König. References[edit] Kosmann-Schwarzbach, Yvette (2010), The Noether theorems: Invariance and conservation laws in the twentieth century, Sources and Studies in the History of Mathematics and Physical Sciences, Springer-Verlag, ISBN 978-0-387-87867-6 Olver, Peter (1993), Applications of Lie groups to differential equations, Graduate Texts in Mathematics 107 (2nd ed.), Springer-Verlag, ISBN 0-387-95000-1 External links[edit] English translation of Noether's paperFulp, R., Lada, T., Stasheff, J..
Mathematical physics - Is there something similar to Noether's theorem for discrete symmetries? Put into one sentence, Noether's first Theorem states that a continuous, global, off-shell symmetry of an action S implies a local on-shell conservation law.
By the words on-shell and off-shell are meant whether Euler-Lagrange equations of motion are satisfied or not. Now the question asks if continuous can be replace by discrete? It should immediately be stressed that Noether Theorem is a machine that for each input in form of an appropriate symmetry produces an output in form of a conservation law. Bloch wave. Isosurface of the square modulus of a Bloch wave in silicon lattice Solid line: A schematic of a typical Bloch wave in one dimension.
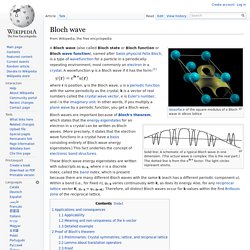
(The actual wave is complex; this is the real part.) The dotted line is from the eik·r factor. The light circles represent atoms. A Bloch wave (also called Bloch state or Bloch function or Bloch wave function), named after Swiss physicist Felix Bloch, is a type of wavefunction for a particle in a periodically-repeating environment, most commonly an electron in a crystal.
These Bloch wave energy eigenstates are written with subscripts as ψn k, where n is a discrete index, called the band index, which is present because there are many different Bloch waves with the same k (each has a different periodic component u). Applications and consequences[edit] Bloch wave. Isosurface of the square modulus of a Bloch wave in silicon lattice Solid line: A schematic of a typical Bloch wave in one dimension.
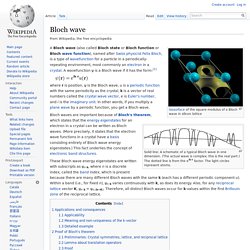
(The actual wave is complex; this is the real part.) The dotted line is from the eik·r factor. The light circles represent atoms.