

New Tab. Hexagonal Grids. This page includes interactive diagrams that require your browser to have SVG and Javascript enabled.
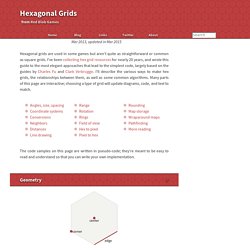
Hexagons are 6-sided polygons. Regular hexagons have all the sides (edges) the same length. I’ll assume all the hexagons we’re working with here are regular. The typical orientations for hex grids are horizontal () and vertical (). Hexagons have 6 edges. Angles In a regular hexagon the interior angles are 120°. Function hex_corner(center, size, i): var angle_deg = 60 * i + 30 var angle_rad = PI / 180 * angle_deg return Point(center.x + size * cos(angle_rad), center.y + size * sin(angle_rad)) To fill a hexagon, gather the polygon vertices at hex_corner(…, 0) through hex_corner(…, 5). The difference between the two orientations is that x and y are swapped, and that causes the angles to change: angles are 0°, 60°, 120°, 180°, 240°, 300° and angles are 30°, 90°, 150°, 210°, 270°, 330°.
Size and Spacing Next we want to put several hexagons together. Switch to or back to hexagons. Geometry with Hex Coordinates. \newcommand{\bv}[1]{{\bf #1}} \newcommand{\bperp}{{\bf perp}} \newcommand{\bproj}{{\bf proj}} There is surprising little information available on hex-coordinates, despite how many games use hex grids.
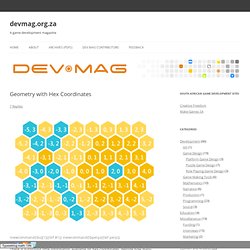
In this article I will explain some of the math so that you can do basic geometry in a hex grid, and design more elegant algorithms for your hex-grid games. There are different coordinate systems for hexes of course. (For a very informative explanation, with many interactive examples, see Amit Patel’s wonderful guide Hexagon Grids.) We will work with an axial coordinate system, which is illustrated in the figure below. From time to time we will use an extra coordinate.
Z = -(x + y) So in fact x + y + z = 0. Here I will use both notations [x, y, z] and [x, y] to denote the same point. Hexagonal Engineering - Honeycomb Page. Hexagon grids: coordinate systems and distance calculations at keekerdc. A big challenge that loomed when I embarked on the Statecraft was proper implementation of a hexagon grid.

I felt the move to a hex grid was one of the few things that Civ V actually got right, and had the potential to bring a more interesting military layer to the game. Unfortunately, it was done at the expense of…everything else. Taking specific gameplay mechanics aside however, a poorly implemented hex grid, at the base technical level, has the potential to create massive headaches for me (the programmer) and millions of wasted CPU cycles.
The reason for this is the very nature of trying to assign Cartesian coordinates to a honeycomb grid. Quite frankly, all the existing works browsable through Google searches on the subject of coordinate systems on hex grids are pretty piss poor, needlessly complex, or just flat out wrong; I would have to tackle the topic myself. First things first, square grids. Hexagonal grid: Generating the grid « Turn-based RPG with Unity. Why hexagonal grid is better than square grid If even such well established strategy franchise like “Civilisation” adapted hex grids in their latest game, there should be a good reason to use them, right?
Well, there are a couple of good reasons why people choose hex grids. Hexagonal grid: Path-finding using A* algorithm « Turn-based RPG with Unity. Public GameObject Line; List<GameObject> path; void Start() setSizes(); createGrid(); generateAndShowPath(); void createGrid() Vector2 gridSize = calcGridSize(); GameObject hexGridGO = new GameObject("HexGrid"); Dictionary<Point, Tile> board = new Dictionary<Point, Tile>();
Hex Grid Algorithm Testbed. DaviesTilePattern - chc61 - The tiling pattern devised by Donald Davies for the entrance hall floor of the Charles Babbage Building. - Website entry for CHC61 webdesign competition. The tiling pattern devised by Donald Davies for the entrance hall floor of the Charles Babbage Building, home of much of NPL's computing work from 1964 to 1996.
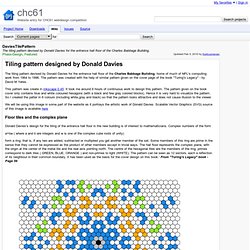
The pattern was created with the help of similar pattern given on the cover page of the book "Turing's Legacy" - by David M Yates. This pattern was create in Inkscape 0.45. It took me around 6 hours of continuous work to design this pattern. The pattern given on the book cover only contains blue and white coloured hexagons (with a black and few gray colored blocks). Hence it is very hard to visualize the pattern. We will be using this image in some part of the website as it portrays the artistic work of Donald Davies.
Hexagonal tiling. In geometry, the hexagonal tiling is a regular tiling of the Euclidean plane, in which three hexagons meet at each vertex.
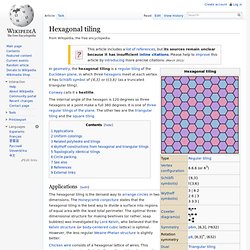
It has Schläfli symbol of {6,3} or t{3,6} (as a truncated triangular tiling). Conway calls it a hextille. The internal angle of the hexagon is 120 degrees so three hexagons at a point make a full 360 degrees. It is one of three regular tilings of the plane. The other two are the triangular tiling and the square tiling. Applications[edit] The hexagonal tiling is the densest way to arrange circles in two dimensions. Chicken wire consists of a hexagonal lattice of wires. Programming for fun: Hex grids. Geometry.
Gd reflections: Hexagonal grid math. Uniform hexagonal grid is a recurring pattern in computer games and graphics applications.

There are few operations one might need to perform: finding hexagon's position by its index in the grid;picking a hexagon by mouse;finding neighbor cells;finding hexagon's corner coordinates etc. While these things do not appear hard at all (something like primary school-level geometry/arithmetics), it's not as straightforward as with a rectangular grid, hovewer. Having tried to consult with internets I've found a neat article on CodeProject, which was solving exactly the problems mentioned. It's considerably highy rated, which I guess means that this stuff is indeed in demand.
What have confused me, though, is that presented solution (and code) seemed to be more complex than one could expect: