

Faculty.cs.tamu.edu/schaefer/research/lofting.pdf. Fundamentals of Transportation/Horizontal Curves. Horizontal Curves are one of the two important transition elements in geometric design for highways (along with Vertical Curves).
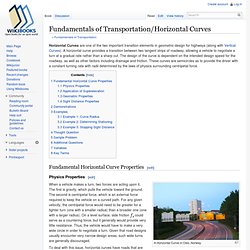
A horizontal curve provides a transition between two tangent strips of roadway, allowing a vehicle to negotiate a turn at a gradual rate rather than a sharp cut. The design of the curve is dependent on the intended design speed for the roadway, as well as other factors including drainage and friction. These curves are semicircles as to provide the driver with a constant turning rate with radii determined by the laws of physics surrounding centripetal force. Fundamental Horizontal Curve Properties[edit] Physics Properties[edit] A Horizontal Curve in Oslo, Norway. B-spline/NURBS Curves: Knot Insertion. The meaning of knot insertion is adding a new knot into the existing knot vector without changing the shape of the curve.
This new knot can be equal to an existing one and in this case the multiplicity of that knot is increased by one. Because of the fundamental equality m = n + p + 1, after adding a new knot, the value of m is increased by one, and, consequently, either the number of control points or the degree of the curve must also be increased by one. Changing the degree of the curve will change the shape of the curve globally and will not be considered. Therefore, inserting a new knot causes a new control point to be added. In fact, some existing control points are removed and replaced with new ones by corner cutting. Although knot insertion looks not very interesting, it is one of the most important algorithms for B-spline and NURBS curves since many other useful algorithms will be based on knot insertion. Inserting a Single Knot where the ratio ai is defined below: Math - How to remove a node of a Bezier curve so that the shape of the curve does not change.
1.4.3 Algorithms for B-spline curves. Bézier curves - a primer. Preface In order to draw things in 2D, we usually rely on lines, which typically get classified into two categories: straight lines, and curves.
The first of these are as easy to draw as they are easy to make a computer draw. Give a computer the first and last point in the line, and BAM! Faculty.cs.tamu.edu/schaefer/research/slides/LRNonUniformTalk.pdf. Draw a Smooth Curve through a Set of 2D Points with Bezier Primitives. Download source code - 26.12 KB Introduction From time to time, I am faced with the question: how to draw a smooth curve through a set of 2D points?
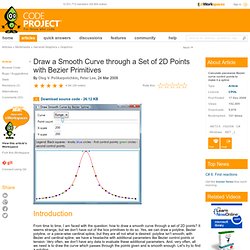
It seems strange, but we don't have out of the box primitives to do so. Yes, we can draw a polyline, Bezier polyline, or a piece-wise cardinal spline, but they are all not what is desired: polyline isn't smooth; with Bezier and cardinal spline, we have a headache with additional parameters like Bezier control points or tension. Very often, we don't have any data to evaluate these additional parameters. Www.handwritten.net/mv/papers/shao96curve_fitting_with_bezier_cubics.pdf. 948762381/04. Cadcam.eng.sunysb.edu/~purwar/Teaching/MEC572/Term_Papers/Yajie_Liu_Term_Paper.pdf. Www.circuitwizard.de/tpic2pdftex/bezier.pdf. Itc.ktu.lt/itc354/Riskus354.pdf. Www.tsplines.com/resources/class_notes/Bezier_curves.pdf. Thinking About Bézier Curves. Thinking About Bézier Curves Recently, in an interactive graphics project, I needed to animate some sprites along a Bézier Curve.

There are many APIs available in interactive applications which provide Bézier Curves for the programmer to use. However, I needed to derive tangents, normals, and other elements from the Bézier Curve, so it was time to dig in and roll my own Bézier Curve objects and functions. I have worked with Bézier Curves for a long time, but I never understood how they actually worked under the hood.
During my investigation I discovered a lot of interesting information about these mathematical objects. It's quite easy to find information about Bézier Curves on the Internet. Linear Interpolation According to Wikipedia, interpolation "...is a method of constructing new data points within the range of a discrete set of known data points. " So how is interpolation actually accomplished?
Center of Mass /* calculate the center of mass */ Summary. Guru's Lair: Cubic Spline & Bezier Curves Library. Spline Interpolation Demo. Click on and move around any of the points that are being interpolated.
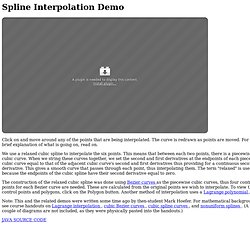
The curve is redrawn as points are moved. For a brief explanation of what is going on, read on. We use a relaxed cubic spline to interpolate the six points. This means that between each two points, there is a piecewise cubic curve. When we string these curves together, we set the second and first derivatives at the endpoints of each piecewise cubic curve equal to that of the adjacent cubic curve's second and first derivatives thus providing for a continuous second derivative. The construction of the relaxed cubic spline was done using Bezier curves as the piecewise cubic curves, thus four control points for each Bezier curve are needed. Note: This and the related demos were written some time ago by then-student Mark Hoefer. Sketchsource.
Bezier curves - a primer. In order to draw things in 2D, we usually rely on lines, which typically get classified in to categories: straight lines, and curves.

The first of these are as easy to draw as they are easy to make a computer draw. Give a computer the first and last point in the line, and BAM! Straight line. No questions asked. Curves, however, are a much bigger problem. They're named after Pierre Bézier, who is principally responsible for getting them known to the world as a curve well-suited for design work (working for Rénault and publishing his investigations in 1962), although he was not the first, or only one, to "invent" these type of curves.
So, what if you need to program them yourself? All Bézier graphics are interactive. This page uses Processing examples, rendering as interactive graphics on the page using Processing.js, which means you don't need any plugins if you're on a modern browser.