

Équation du second degré. ChronoMath, une chronologie des MATHÉMATIQUESà l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Une telle équation est de la forme : ax2 + bx + c = 0 où a, b et c sont des nombres réels ou complexes donnés, a étant non nul.

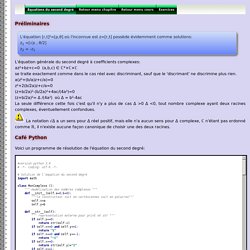
Le membre de gauche est un polynôme du second degré : c'est un trinôme (trois termes) du second degré. Des résolutions partielles de cette équation apparaissent au fil des âges (en particulier avec Al-Khwarizmi et Abu Kamil au 9è/10è siècle, Savasorda au 11è siècle). L’équation du second degré : résolution algébrique. L’équation du second degré : interprétation géométrique. L’équation du second degré : illustration. Equations du second degré. Préliminaires L'équation [r,t]²=[ρ,θ] où l'inconnue est z=[r,t] possède évidemment comme solutions: z1 =[√ρ , θ/2] z2 = -z1 L'équation générale du second degré à coefficients complexes: az²+bz+c=0 (a,b,c) ∈ ℂ*×ℂ×ℂ se traite exactement comme dans le cas réel avec discriminant, sauf que le 'discrimant' ne discrimine plus rien.
Nappe module de P(z) Résolution des équations de degré 3 et 4. Ce texte — qui reprend un exposé du séminaire Mathematic Park donné par l’auteur en octobre 2011 à l’occasion des célébrations du bicentenaire de la naissance d’Évariste Galois — propose de montrer quelques aspects de la résolution des équations algébriques de degré 3 et 4 à travers une petite promenade mathématique qui commence au XVIème siècle avec les mathématiciens de la Renaissance italienne et se termine au XVIIIème siècle avec les travaux de Lagrange.
Introduction Avant d’aborder la résolution des équations proprement dite, il est nécessaire de préciser de quelles équations on parle et ce que l’on entend par « résolution ». Qu’est-ce qu’une équation algébrique ? FICHE EQDEGRE3. LMBparaboleaire. Polynômes 1 : définition. JMCFP alg ruffini. Méthode de Ruffini-Horner. En mathématiques et algorithmique, la méthode de Ruffini-Horner, connue aussi sous les noms de méthode de Horner, algorithme de Ruffini-Horner ou règle de Ruffini, se décline sur plusieurs niveaux.
Elle permet de calculer la valeur d'un polynôme en x0. Elle présente un algorithme simple effectuant la division euclidienne d'un polynôme par X - x0. Mais elle offre aussi une méthode de changement de variable X= x0 + Y dans un polynôme. C'est sous cette forme qu'elle est utilisée pour déterminer une valeur approchée d'une racine d'un polynôme. Histoire[modifier | modifier le code] En tant que technique de changement de variable, on retrouve des algorithmes analogues, en Chine, pour l'extraction de racine n-ième, dans les Neuf Chapitres (263 apr.
Valeur d'un polynôme en un point[modifier | modifier le code] Soit un polynôme[6] et x0 un nombre[7]. La méthode consiste donc à multiplier le premier coefficient par x0 et à lui ajouter le deuxième coefficient. Ce nombre vaut Si on écrit Soit encore Donc. Calcul d'une parabole par la méthode de Cramer.
Équations du quatrieme degré. Forme canonique Nous nous attaquons maintenant fort logiquement au degré supérieur, c'est à dire le degré 4.
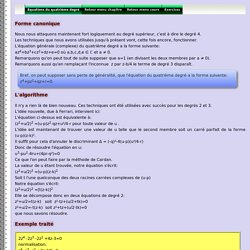
Les techniques que nous avons utilisées jusqu'à présent vont, cette fois encore, fonctionner. L'équation générale (complexe) du quatrième degré a la forme suivante: az4+bz3+cz2+dz+e=0 où a,b,c,d,e ∈ ℂ et a ≠ 0. Remarquons qu'on peut tout de suite supposer que a=1 (en divisant les deux membres par a ≠ 0). Remarquons aussi qu'en remplaçant l'inconnue z par z-b/4 le terme de degré 3 disparaît. Bref, on peut supposer sans perte de généralité, que l'équation du quatrième degré a la forme suivante: z4+pz2+qz+r=0. L'algorithme Il n'y a rien là de bien nouveau. Exemple traité. Racinesdeuxtheoremes.
TFARMS.
Polynomes.