

N. Pouyanne - A propos de modélisation en mathématiques au lycée - PeerTube. Mathématiques et justice : les formules ont-elles un rôle à jouer dans les procès criminels ? - WebTV Université de Lille. Modelisation mathematique. Mathématiques, modélisation et simulation - Université de tous les savoirs. Pierre-Louis Lions est un mathématicien français né à Grasse en 1956, lauréat de la médaille Fields en 1994.Fils du mathématicien Jacques-Louis Lions, Pierre-Louis Lions entre à l'École normale supérieure (Paris) en 1975.
Refusant de passer l'agrégation de mathématiques, il préfère se consacrer à la recherche en mathématiques appliquées et obtient son doctorat en 1979 à l'Université Pierre et Marie Curie[1]. De 1979 à 1981, il poursuit ses recherches au CNRS puis devient professeur à l'université de Paris-Dauphine. Modelisation mathematique JCDr.
Modèles mathématiques. Conférence de J.J. DAHAN à l’Alliance Française de Lagos 1. Michele Artigue Rouen 2008. MPTUne breve par jour. Multimedia518. Modélisation statistique. Modèles et calculs combinatoires. De combien de façons peuvent être distribuées les 32 cartes d’un jeu de belote ?

De combien de façons pouvons-nous obtenir 13 en sommant les résultats de 3 dés ? De combien de façons peut être mélangé un paquet de n cartes ? L’ambition de la combinatoire énumérative est de compter le nombre (fini) de combinaisons dans ce type de situation. La motivation pour envisager tous les cas possibles n’est pas toujours ludique. De combien de façons peut s’exécuter ce programme ? Un exemple de calibrage : observer une centaine d’individus pris au hasard dans une population humaine incite à fixer la hauteur des portes à environ 2,05 m, pour peu qu’on évite les rassemblements de basketteurs professionnels ou bien de gymnastes olympiques.
Ce texte propose une promenade dans des exemples d’énumérations combinatoires. Un premier exemple, issu de l’étude d’un polymère Notre premier modèle se trouve en physique statistique et considère un polymère au voisinage d’une paroi. Lubsanski. Modélisation. Vous trouverez ici quelques documents en lien avec les mathématiques dans les autres disciplines et la modélisation.

L'acronyme DFF se rapporte au Master Didactique et formation des formateurs des universités Versailles-St Quentin et Paris-Diderot. Si certains documents ne sont pas en ligne ... contactez-moi ! ADN : génétique des populations (atelier, APMEP, Orléans), mémoire de Master sur la dérive génique (N. Erard, C. Fauvé, C. Expose saad lycee. Carbon Dioxide Pumphandle 2019. Maths et courants marins. Ressources scientifiques - maëlle nodet. Sur cette page vous trouverez un aperçu de mes activités de popularisation des maths et de la science, à destination du grand public, des scolaires et des enseignant·es du secondaire.
Dès que possible, je propose aussi les ressources créées pour ces occasions (sous les termes de la licence CC BY-NC-SA 4.0). Océans et courants marins Mathématiques pour la planète terre En 2013 a eu lieu l’opération Mathématiques pour la planète terre, qui a donné lieu à de nombreuses manifestations à destination du grand public et des scolaires. Avec Antoine Rousseau et Sebastian Minjeaud, nous avons contribué à cette opération en proposant une activité autour des courants marins, qui s’est déclinée sous plusieurs formes différentes : Un article sur Interstices intitulé Comprendre la circulation océanique (avec A.
Des maths pour l’environnement - WebTV Université de Lille. Abboud Terrasse. Philippe Thieullen. K1MA6W14 : Biomodélisation Cours d'introduction : (Le cours suit en partie les livres de L.J.S.

Comprendre la circulation océanique. Il existe, sous la surface de nos océans, un immense réseau de courants marins, sortes de tapis roulants des mers, qui transportent des masses d’eau absolument gigantesques.
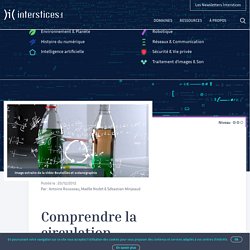
Bien que la cartographie de ces courants soit extrêmement complexe, des processus physiques très simples permettent d’en expliquer les grandes lignes. Ces courants à grande échelle, parmi lesquels figure le célèbre Gulf Stream, jouent un rôle primordial dans la dynamique des océans, et bien entendu dans l’équilibre thermodynamique de notre planète. Il est donc essentiel de pouvoir les comprendre afin d’anticiper d’éventuels déséquilibres qui pourraient advenir, par exemple, dans le cadre du réchauffement climatique.
Modéliser et simuler la fonte des calottes polaires. Le niveau des mers monte, pour différentes raisons liées au réchauffement climatique.
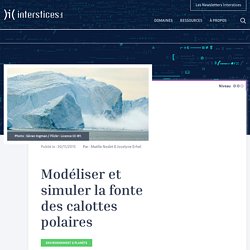
Les glaciers de l’Antarctique et du Groenland, qu’on appelle calottes polaires ou inlandsis, jouent un rôle majeur dans l’évolution du niveau des mers. Peut-on prévoir l’évolution future de ces calottes polaires et en particulier le vêlage d’icebergs dans l’océan ? Cet article est à l’origine du module « Simuler la fonte des calottes polaires » primé lors de la compétition internationale des Mathématiques de la planète Terre. La contribution des calottes polaires à la montée du niveau des mers est essentiellement la combinaison de trois phénomènes : Animation réalisée par Victoria Denys. Les épisodes de vêlage d’icebergs peuvent être particulièrement spectaculaires, comme le montre cette vidéo (en anglais) sur le glacier Jakobshavn au Groenland.
Maximath. Zago. Publication.html. Abstract: SORTIE is a forest simulator developed by Pacala, Ribbens, Kobe et al. in 1993-1996.

It is based on the forest data observed in and around Great Mountain Forest (GMF), a privately owned 2500ha forest located in northwestern Connecticut (41°57'N, 73°15'W), USA in the year 1990-1992. SORTIE is an individual based model (IBM). It consists of four submodels (resource, growth, mortality, and recruitment) to determine the behavior of each individual, from which the behavior of the whole forest community can be determined. The main ingredient taken into account in SORTIE is the competition for light between trees. In [1] we build a mathematical model (a state-dependent delay differential equation derived from a size-structured model) for the adult population of trees A(t) in two cases (single species case and two-species case) and we compare it with SORTIE.
Publication.html. Publication.html. Publication.html. Workshop Modeling the propagation of Covid-19. Monday 18 to Wednesday 20 May 2020 – videoconference.

– Editeur de MATLAB et Simulink - MATLAB & Simulink. Modélisation de la croissance des micro-organismes - Inria. Laurent Dumas-Professeur des Universites- Universite de Versailles. Une approche mathématique pour révolutionner la gestion de l’eau - WebTV Université de Lille. Page personnelle d'Olivier Garet. Percolation.

PHÉNOMÈNES D'ALIGNEMENT BANCS DE POISSONS, NUÉES D'OISEAUX (...) - Frouvelle - Math Park - 16/03/19. CIRM - Videos & books LibraryDocuments : Modélisation mathématique en lien avec le stockage des déchets radioactifs. Modélisation & Simulation. Modélisation & Simulation La forme idéale d’une aile Régis Duvigneau Niveau intermédiaire Niveau 2 : Intermédiaire La forme idéale d’une aile Lire l’article Environnement & Planète.
Vidéos » modélisation - WebTV Université de Lille. Cours NuagesPoints3D presentation10 2019. M1 SI. Tamy Boubekeur's Homepage. Fabrizio Corda, Jean Marc Thiery, Marco Livesu, Enrico Puppo, Tamy Boubekeur and Riccardo Scateni. Maths dev. Penser, modéliser et maîtriser le calcul informatique - Algorithmes, machines et langages - Gérard Berry - Collège de France - 19 novembre 2009 18:00. Berry09 Inaugurale public. Le monde est-il écrit en langage mathématique ? Mathématiques, un dépaysement soudain - Pierre-Yves Oudeyer - Interview - 2011. Diapo erhenfest. ModelisationMath. Pratique de la modélisation Statistique. Un modèle mathématique pour décrire les dynamiques des coraux face aux changements climatiques. PSMIR 1999 2000 3 A6 0. Cachan Modélisation. Peut-on modéliser une foule mathématiquement? Fouloscopie.
Berestycki Henri - "Alan Turing et la morphogenèse" - 2008. Né en 1912 en Angleterre, figure mythique des mathématiques du XXème siècle, Alan Turing est connu d'abord pour son travail fondateur de 1936 en logique mathématique, dans lequel il invente les « machines » qui portent son nom. Machines abstraites qui permettent de résoudre des problèmes de logique, elles préfigurent aussi les ordinateurs.
Pendant la seconde guerre mondiale, il travaille pour l'armée britannique au déchiffrage des codes secrets des transmissions de l'armée allemande en apportant plusieurs contributions décisives. Il dirige l’équipe qui parviendra à lire les messages de la marine allemande de l’Atlantique codés par la machine Enigma. Poursuivant après 1945 ses réflexions sur les machines abstraites et le fonctionnement de la pensée, il travaille à des questions qui relèvent de ce qu'on appellerait aujourd'hui l’intelligence artificielle sur la conception d’une machine pensante, capable d’apprendre.
En cela, il est l’un des fondateurs de l’informatique moderne. Modélisation de mouvement de foule (Bertrand Maury) TPE Mouvement de foule. Images des mathématiques. Flots de gradient Considérons une personne perdue dans la montagne en plein brouillard, qui cherche à rejoindre la vallée au plus vite. On peut imaginer qu’elle tâtonne autour d’elle pour estimer dans quelle direction aller (en l’occurrence la direction de plus grande pente), fait un ou plusieurs pas dans cette direction, puis recommence le processus. Pour formaliser cette démarche, on décrit le profil de la montagne par une fonction $f({\bf x})$ qui représente l’altitude au point ${\bf x}$ du plan (on peut voir ce point ${\bf x}$ comme le couple latitude-longitude qui positionne un point à la surface du globe).
Si l’on numérote par $1$, $2$,..., $n$,... les instants auxquels elle fait le point et par ${\bf x}_1$, ${\bf x}_2$,..., ${\bf x}_n$ les positions correspondantes, le parcours de notre promeneur est défini par \[ {\bf x}_{n+1} = {\bf x}_{n} -h \nabla f ({\bf x}_{n}), \] où $h$ est un paramètre qui quantifie la taille des pas. Modèle de foule Conclusion. Simulation de foule (prototype) Mathématiques et Mouvements de foules - Bertrand Maury. Ecoulement granulaires par le µ(I) Ecoulements Granulaires Secs avec la Rhéologie du µ(I) Lagrée P.
-Y., ∂'Alembert, CNRS, UPMC; www.lmm.jussieu.fr/~lagree voir aussi la page de Lydie Staron www.lmm.jussieu.fr/~staron Vision continue des matériaux granulaires, le µ(I) Mais un autre point de vue existe, il consiste à oublier les grains en regardant d'un peu loin le tas de grains. On parle alors d'approche continue (cette approche est naturelle, en effet, des milieux solides ou fluides tels que l'acier et l'eau sont considérés comme continus alors qu'ils sont constitués d'atomes). Des approches existent en partant de l'état solide et d'autres en partant de l'état liquide, les deux n'étant pas encore vraiment fusionnées. Mouvement Brownien. Images des mathématiques. Les modèles d’évolution de populations ont une longue histoire [1]. La suite de Fibonacci fut introduite au XIII^e siècle par Léonard de Pise pour décrire la croissance d’une population de lapins.
Le modèle le plus connu d’évolution de populations est sans doute celui de Malthus, proposé au début du XIX^e siècle. Supposons que chaque année, 15\% des individus de la population donnent naissance à un enfant, et que 5\% meurent. Modéliser plus pour simuler moins. À l’occasion du colloque « Modélisation : succès et limites », le chercheur Frédéric Alexandre nous éclaire sur les développements actuels de la simulation et de la modélisation.
Frédéric Alexandre, vous êtes chercheur au Laboratoire bordelais de recherche en informatique (LaBRI1) et intervenant du colloque « Modélisation : succès et limites » qui se tient le 6 décembre 2016. Qu’entend-on au juste aujourd'hui par modélisation et simulation ? F. A. : La dimension numérique s'est intensément développée dans tous les domaines où l'on sait représenter les phénomènes par des équations que l'on peut ensuite implanter informatiquement – on parle alors de modèles de connaissance. Ce phénomène s’est amplifié, surtout dernièrement avec la possibilité d'utiliser les données massives (big data) et l’apprentissage automatique (machine learning) pour faire des statistiques – on parle dans ce cas de modèles de représentation. Demailly Jean-Pierre - "La découverte de Fourier : même le feu est régi par les nombres" - 2011.
Marie Théret - Au Feu ! L'agriculture croît dans les mathématiques. Réduction des pesticides et engrais, prédiction des récoltes, adaptation au changement climatique... Les défis posés à l’agriculture sont multiples et les mathématiciens ont des solutions à apporter. Focus sur leurs travaux à l'occasion du Salon de l'agriculture qui se tient à la Porte de Versailles jusqu'au 3 mars. Peut-on mettre l’agriculture en équations ? C’est le défi que tentent de relever depuis plusieurs années déjà les mathématiciens, qui mobilisent pour cela tout un arsenal - modélisation, statistiques, traitement d’image... Simulation de la croissance de plantes (betterave, Arabidopsis, blé, riz, maïs, tournesol, chrysanthème, concombre, tomate, poivron, caféier, pin) par le logiciel Digiplante du laboratoire de mathématiques et informatique de CentraleSupélec.
Prédire la récolte grâce aux modèles. Agriculture : des logiciels pour les «circuits courts» Il ne suffit pas de décréter qu’on va manger local. Encore faut-il que les agriculteurs soient organisés pour cela et y trouvent leur compte financièrement. Des chercheurs en informatique se sont penchés sur l’optimisation des circuits courts, qui mettent directement en contact clients et producteurs. Manger local grâce aux circuits courts. C’est ce que demandent de plus en plus de consommateurs, qui n’hésitent plus à acheter directement auprès des agriculteurs de leur région.
D’où vient la forme des arbres? Ils étudient les cyclones grâce à des bulles de savon. Le développement a rendez-vous avec les mathématiques. Comment les mathématiques peuvent-elles accompagner les pays en développement ? À l'occasion de la conférence internationale Maths Day for Developpement, organisée à Paris, le 15 mars, Mohammed Jaoua, mathématicien tunisien et acteur de la scène scientifique internationale, nous donne quelques éléments de réponse.
Si les mathématiques permettent de mieux comprendre le monde qui nous entoure, elles participent également à son évolution. À travers les algorithmes et l’intelligence artificielle, mais également par l’étude et la compréhension de phénomènes telles l’érosion des sols, la montée des océans ou encore la gestion de la pêche. Ces enjeux, majeurs pour le développement économique d’un pays, nécessitent des outils mathématiques de plus en plus sophistiqués. Quelle est aujourd’hui la place des mathématiques dans les pays en développement ? Cours de mathématiques dans l’enseignement supérieur à l’Université du Sahel, à Bamako au Mali. Le grand incendie d’Aullène simulé à la flamme près. En 2013, une équipe de chercheurs français a effectué la simulation complète d’un immense incendie de forêt avec une précision inégalée. Nous sommes en juillet 2009.
Quand les maths se mêlent de sport. Des équations pour améliorer les performances sportives, du sport pour éclairer les phénomènes physiques… Et si les chercheurs et les sportifs avaient beaucoup à se dire ? Toucher le virtuel. Comment calculer le prix du calcul. Le nouveau supercalculateur Jean-Zay, installé à l’Idris, centre de calcul intensif du CNRS, est un des ordinateurs financés et mis à la disposition de la recherche française. Maimosine met le monde en modèles. Modélisation. Marine Fontaine - Euler et Cie. Mallat Stéphane - "Mystères mathématiques de l'apprentissage par réseaux de neurones" - 2017.
Laumond Jean-Paul - "Poincaré et la robotique : la géométrie pour agir par le mouvement" - 2017. Saint-Raymond Laure - "Décrire mathématiquement les gaz : le défi de Boltzmann" - 2010. Barbara Schapira - La menace du stéréotype. LA NAISSANCE DE LA THÉORIE DE L'INFORMATION OU LA FORCE D'UNE IDÉE SIMPLE. Les crises stratégiques (et leurs modèles mathématiques) - WebTV Université de Lille. Quelques réflexions sur l’usage de la photographie et du cinéma dans la balistique du XXe siècle à partir des travaux expérimentaux de J. Kampé de Fériet et de Gabriel Foëx (1915-1925) - WebTV Université de Lille. L’expérimentation, modélisation et conceptualisation - WebTV Université de Lille. Math Park - 10/03/2018 - Irène MARCOVICI - AUTOMATES CELLULAIRES ET CORRECTION D'ERREURS. Math Park - 13/05/2017 - DOMINIQUE PICARD, QUELQUES PARADIGMES MATHÉMATIQUES (...)
Synthèse d'images - modélisation géométrique - IUT d'Arles. Un double numérique pour Notre-Dame. Mathematical imagery - WebTV Université de Lille. Visualizing Algorithms. Compression JPEG. Mathématiques et biodiversité. Leçon n°10 : la modélisation. Www-ljk.imag.fr/membres/Jean-Guillaume.Dumas/Publications/ComplexesSimpliciaux/Diapositive01.html. L'approche calculatoire des neurosciences - Algorithmes, machines et langages - Alexandre Pouget - Collège de France - 23 mai 2008 11:30.