

Chapitre 2 Equations cartésiennes de droites. Chapitre 3 Statistiques 1S. Module Algo de Tri. Chapitre 4 Signes du trinôme. Chapitre 5 Angles orientés. Chapitre 6 Fonctions associées. Chapitre 7 Variables aléatoires. Chapitre 8 Suites numériques. Chapitre 9 Nombre dérivé. Chapitre 10 Cosinus et sinus d'un réel. Chapitre 11 Schémas de Bernoulli et arbres. Chapitre 12 Fonction dérivée. Chapitre 13 Produit Scalaire. Chapitre 14 Suites arithmétiques et géométriques. Chapitre 15 Loi Binomiale.
Cours de mathématiques de première S. Maths première. Première S - Cours et Exercices. Quelques contrôle de Première S. 1 Quelques contrôle de Première S Gilles Auriol http ://auriolg.free.fr Voici l énoncé de 7 devoirs de Première S, intégralement corrigés.
Malgré tout les devoirs et 5 nécessitent l usage du théorème des valeurs intermédiaires, ils conviendront certainement mieux à la classe de Terminale S. 2 Contrôle d été - Épisode. Soit g : x x 3 + x x 5 et C g sa courbe représentative dans un repère orthonormé. (a) Limites aux bornes de l ensemble de définition, dérivée, tableau de variation avec valeurs des extrémums locaux. (b) Déduire du tableau de variation qu il existe un unique réel α tel que g(α) = 0. 3 Correction du contrôle d été - Épisode.
Manuel 1èreS. SommaireMéthodesA1A2A3A4A5A6POG1G2G3SP1SP2SP3Fiches TICESolutionsLexiqueRabats Sommaire des chapitres du manuel.

Sommaire des méthodes de l'année. Chapitre : Second degré Chapitre : Fonctions de référence Chapitre : Dérivation Chapitre : Applications de la dérivation Chapitre : Notion de suite. (1) Maths en tête - Alexandre Morgan. Format Cours 1ère - Trigonométrie (cercle trigo et enroulement de l'axe des réels) TRIGONOMÉTRIE - Lire les angles remarquables sur le cercle - Première. Mémo - Le cercle trigonométrique. Première maths spécialité (méthode) : "Déterminer la mesure principale d'un angle" Replay Cours 1ère - Trigonométrie. Replay Cours 1ère - Fonctions Trigonométriques Partie 1. Replay Cours 1ère - Fonctions Trigonométriques - Partie 2. Inéquations trigonométriques. Mode d'emploi Dans la première partie vous devez colorier en vert les points du cercle trigonométrique associés aux solutions de l'inéquation proposée.

Les extrémités des arcs sont représentables de deux manières ou suivant qu'elles appartiennent ou n'appartiennent pas à l'arc. Cliquez sur l'une des huit images situées à droite de la figure pour choisir le type d'arc de cercle voulu, puis déplacez le point rouge pour modifier la longueur de l'arc. , validez par exemple , puis cliquez sur pour obtenir l'affichage : Pour saisir l'ensemble des solutions utilisez le clavier virtuel proposé: Dans le bas de la figure vous pouvez si vous le voulez tracer la courbe de la fonction utilisée dans l'inéquation, mais ceci n'est pas obligatoire. Voir la vidéo de démonstration. Loi des Sinus.
La loi des sinus. Théorèmes du sinus et du cosinus. Théorème de cosinus. La loi des sinus (Trigonométrie XVIII) Al Kashi. Al Kashi) Biographie de Jamshid al-Kashi. Jamshid al-Kashi est un mathématicien et astronome perse.
Il est le dernier grand savant du monde arabe avant que l'Occident, à la Renaissance, ne prenne le relais. Il est né vers 1380 à Kashan, dans le nord ouest de l'Iran. Son enfance se déroule alors que l'empereur turco-mongol Tamerlan bâtit un immense empire basé sur la puissance militaire et la terreur. Les conditions de vie sont alors très difficiles à Kashan, mais elles s'améliorent grandement lorsque le fils de Tamerlan, Shah Rook, lui succède en 1405. Il ramène la prospérité économique dans la région et développe la vie artistique et intellectuelle. On a quelques informations fiables sur la vie d'al-Kashi grâce à des lettres qu'il a écrites à son père et qui sont parvenus jusqu'à nos jours. La capitale de l'empire fondé par Tamerlan est Samarcande, en Ouzbekistan. Il calcule π avec une précision égale à neuf chiffres en base 60 (ce qui correspond à 16 décimales). Les entrées du Dicomaths correspondant à Kashi. Théorème de Al-Kashi.
Al Kashi. A cette époque, les scientifiques effectuent leurs recherches à la cours de rois ou de princes.
A Samarkand, al Kashi vit sous la protection du prince Ulugh-Beg (1394 ; 1449) qui a fondé une Université comprenant une soixantaine de scientifiques qui étudient la théologie et les sciences. Il devient Premier Directeur du nouvel observatoire de Samarkand et s’adonne pleinement à ses travaux tout en s’assurant d’être à l’abri du besoin. De nombreux ouvrages d'al Kashi ainsi que certaines lettres écrites à son père ont survécu. De ce fait, les détails de ses travaux sont connus et souvent datés. Dans le traité d'astronomie Khaqani Zij (1413-1414), il donne des tables trigonométriques en se basant sur les tables de Nasir al Din al Tusi (1201 ; 1274). Dans son Traité sur le cercle (juillet 1424), al Kashi calcule le rapport de la circonférence à son rayon pour obtenir une valeur approchée de 2Pi avec une précision jamais atteinte. Bibliographie. Al Kashi et formule des sinus.
Al-Kashi. Biographie[modifier | modifier le code] Contributions[modifier | modifier le code] Astronomie[modifier | modifier le code] Les travaux menés par Ulugh Beg, Qadi-zadeh Roumi, al-Kashi et quelque soixante autres savants aboutirent à la publication des Tables sultaniennes (Zij-é solTâni, en persan), parues en 1437 mais améliorées par Ulugh Beg jusque peu avant sa mort en 1449.
Les données des Khaqani zij y furent bien sûr utilisées. Al-kashi. Ce résultat est porte le nom du mathématicien persan du début du XVe siècle al-Kâshî.
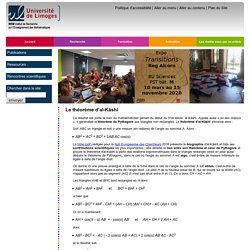
Appelé aussi « loi des cosinus », il généralise le théorème de Pythagore aux triangles non rectangles. Le théorème d'al-Kâshî s'énonce ainsi : Soit ABC un triangle et soit α une mesure (en radians) de l’angle au sommet A. Alors AB2 + AC2 = BC2 + 2AB AC cos(α) La fiche (pdf) rédigée pour la Nuit Européenne des Chercheurs 2016 présente la biographie d'al-Kâshî et liste ses contributions scientifiques les plus importantes ; elle détaille le lien entre son théorème et celui de Pythagore et prouve le théorème d'al-Kâshî à partir des relations trigonométriques dans le triangle rectangle (dont on peut aussi déduire le théorème de Pythagore), dans le cas où l'angle au sommet A est aigu, c’est-à-dire de mesure inférieure ou égale à celle de l’angle droit.
Les triangles AHB et BHC sont rectangles en H donc. Le théorème d'Al Kashi (Trigonométrie XIX) Calcul de cos(2π/5) = 1/2 Phi et pentagone régulier. ChronoMath, une chronologie des MATHÉMATIQUESà l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges A - 2π/5 est la mesure en radians de l'angle au centre interceptant un côté du pentagone régulier.
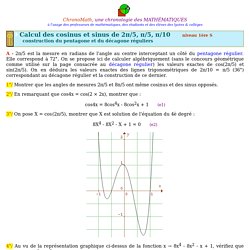
Elle correspond à 72°. On se propose ici de calculer algébriquement (sans le concours géométrique comme utilisé sur la page consacrée au décagone régulier) les valeurs exactes de cos(2π/5) et sin(2π/5). TRIGONOMÉTRIE. PREMIÈRE. SPÉCIALITÉ MATHS. Free Math Worksheets (pdfs) with answer keys on Algebra I, Geometry, Trigonometry, Algebra II, and Calculus. Problèmes trigonométriques (loi des sinus, loi des cosinus) dans le triangle quelconque. Loi des sinus, loi des cosinus dans les triangles quelconques - Trigonométrie. Law of Sines and Cosines, explanation. VERY HARD South Korean Geometry Problem (CSAT Exam) Formule de Mollweide.
Notations usuelles pour un triangle.
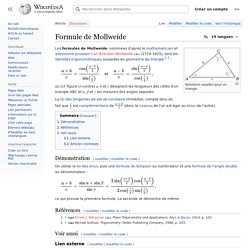
Les formules de Mollweide, nommées d'après le mathématicien et astronome prussien Carl Brandan Mollweide (de) (1774-1825), sont les identités trigonométriques suivantes en géométrie du triangle[1],[2] : où (cf. figure ci-contre) a, b et c désignent les longueurs des côtés d'un triangle ABC et α, β et γ les mesures des angles opposés. Démonstration[modifier | modifier le code] On utilise la loi des sinus, puis une formule de Simpson au numérateur et une formule de l'angle double au dénominateur : ce qui prouve la première formule. Références[modifier | modifier le code] Voir aussi[modifier | modifier le code] Lien externe[modifier | modifier le code] (en) « Mollweide's formula : A proof » [archive], sur math.stackexchange Articles connexes[modifier | modifier le code] Portail de la géométrie.
Calculer une probabilité [en 1min⏱] Les probabilités : répétition d'épreuves indépendantes et variables aléatoires (21 avril) - Vidéo Spécialités. Sophie, prof de maths, propose un cours sur les probabilités et, plus particulièrement, sur la répétition d'épreuves indépendantes et les variables aléatoires.
Retrouvez le support de cours en PDF. Etudier une répétition de deux épreuves indépendantes. Les probabilités conditionnelles et l'indépendance de deux événements (31 mars) - Vidéo Spécialités. Probabilités conditionnelles : type BAC. Replay Cours - 1ère - Probabilités Conditionnelles. Probabilités conditionnelles - appliquer la formule du cours - panne de voiture -Première spé maths♕ PROBABILITÉS CONDITIONNELLES. ÉVÉNEMENTS INDÉPENDANTS. PROBABILITÉS CONDITIONNELLES. PREMIÈRE. BAC. BTS. EXERCICE DE PROBABILITÉ CONDITIONNELLE. BAC. BTS CG. ÉVÉNEMENTS INDÉPENDANTS. PREMIÈRE. BAC. BTS. VARIABLES ALEATOIRES EN PREMIÈRE SPE MATHS. Lire un tableau pour trouver des Probabilités conditionnelles - P(AUB) et P(A∩B) Première spé maths♕ PROBABILITÉS - Formule à connaître - Première. PROBABILITÉS - Formules à connaître (2) - Première. Exercice interactif sur les probabilités conditionnelles. Mathématiques - Comment modéliser une expérience aléatoire ? Une variable aléatoire, c'est quoi ? - best of des aventures d'Albert.
De la moyenne d'une série statistique à l'espérance d'une variable aléatoire (19 mai) - Vidéo Spécialités. Comprendre la formule: E(aX+b)=aE(X)+b. Comprendre la formule et savoir l'utiliser. SC CONDITIONNEMENT TES. Comment démontrer que des événements sont indépendants - Cours et exercice - très IMPORTANT. LE COURS : Probabilités conditionnelles - Première/Terminale. Probabilités conditionnelles : type BAC. Probabilités conditionnelles et arbre pondéré - Exercice très classique - Très IMPORTANT. Modeliser probabilite conditionnelle.
Variable aléatoire : Nombre de chiffres bien placés dans un code. Format Cours 1ère - Variable aléatoire. PROBABILITÉS ET SUITES EN PREMIÈRE SPÉCIALITÉ MATHS. ♕Probabilité évènement indépendant - double six - 3 faces - lancer de dés, pièces Première spé maths. ♕Probabilité de s'arrêter sur un trajet à 2 feux - P(A∩B) épreuve indépendante - première spé maths. Introduction de la fonction exponentielle (2 juin) - Vidéo Spécialités. Dans ce cours, Sophie, la prof de maths, propose une introduction de la fonction exponentielle, une fonction particulière car elle est définit comme la solution d'une équation différentielle. Retrouvez le support de cours en PDF. Rappel sur le nombre dérivé Quand on a une fonction f, on peut la représenter par une courbe.
En tout point de cette courbe, on peut tracer une tangente à la courbe. Au point A, la droite est la meilleure approximation affine de la courbe. Le nombre dérivé est le coefficient directeur (ou pente) de la tangente au point d’abscisse a : f′(a) Fonctions solutions d’une équation différentielle Existe-t-il des fonctions f définies et dérivables sur ℝ telles que, pour tout réel a, f’(a) = a ? → Pour tout réel a le coefficient directeur de la tangente au point d’abscisse a est a. 5 minutes max pour 1 question de BAC - EXPONENTIELLE - RESOLUTION D'EQUATION (1ère Générale)
Fonction exponentielle (1ere) FONCTION EXPONENTIELLE . PREMIÈRE SPÉ MATHS. EXERCICES. FONCTION EXPONENTIELLE PREMIÈRE SPÉ MATHS. FONCTION EXPONENTIELLE - Introduction - Première. Chap 4. La fonction exponentielle Terminale S. Lemme : Si est une fonction dérivable sur R telle que : = et 0! = 1 alors ne s annule pas sur R. 1 Lemme : Si est une fonction dérivable sur R telle que : = et 0! = 1 alors ne s annule pas sur R. La fonction exponentielle. 1 DERNIÈRE IMPRESSION LE 2 novembre 204 à :07 La fonction exponentielle Table des matières La fonction exponentielle 2.
Définition et théorèmes Approche graphique de la fonction exponentielle Relation fonctionnelle Autres opérations Notation Étude de la fonction exponentielle 4 2. Signe Variation Limites Courbe représentative Des ites de référence Étude d une fonction Compléments sur la fonction exponentielle 9 3. Dérivée de la fonction e u Exemples types Fonctions d atténuation Chute d un corps dans un fluide Fonctions gaussiennes PAUL MILAN TERMINALE S 2 TABLE DES MATIÈRES Avant propos Le but de ce chapitre est de construire une des fonctions mathématiques les plus importantes.
Elle est en effet présente dans toutes les sciences. 3 . Fonction Exponentielle. Inéquations et exponentielle - Exercice - Première. Etude d'une fonction avec exponentielle et quotient. Fonction exponentielle - ce qu'il faut savoir pour faire les exercices - très IMPORTANT Terminale S. Mathématiques - Calculer avec la fonction exponentielle. Le nombre e. Programmation Python avec les calculatrices. Des vidés sur les programme Python en première Spécialité maths - Maths & Numérique.