

T. Tokieda : Science à partir d'une feuille de papier. Mathématiques et Origami : le pliage de Miura. Le pliage que nous présentons ici a été développé dans les années 1970 par l'astrophysicien japonais Koryo Miura, dans le but de transporter de façon compacte de larges panneaux solaires, et de les déployer très facilement dans l'espace.

Appliqué à une carte routière, il permet de la plier et de la déplier en un seul mouvement ! À la différence des pliages classiques, une feuille pliée suivant la méthode de Miura ne présente pas de plis orthogonaux : les plis forment un réseau de parallélogrammes, et sont orientés de telle sorte qu'ils sont tous interdépendants. C'est pourquoi rapprocher ou écarter les deux coins opposés de la feuille permet de plier ou déplier en un seul geste. On peut réaliser un pliage avec la méthode de Miura avec un nombre arbitrairement grand de lignes et colonnes (il est toutefois préférable de choisir un nombre de lignes et un nombre de colonnes impairs). Voici quelques détails pour obtenir le pliage, à partir du diagramme de plis ci-dessus. Miura Korio Pliage. Activité Pliage de de Miura. Quand un jouet devient modèle - WebTV Université de Lille.
Images des mathématiques. J’ai passé le dernier weekend de novembre dans le magnifique château de Goutelas.
Ce week-end est traditionnellement organisé pour les étudiants de l’ENS de Lyon. Cette année les cours ont été donnés par Tadashi Tokieda, un mathématicien d’origine japonaise qui travaille à Cambridge et parle parfaitement français (en tous cas, mieux que moi ! ). J’ai aussi testé son niveau de russe et il me paraît très bon. Tadashi est lumineux et attachant, et je pourrais écrire une série de billets seulement sur sa personnalité. Je vais aborder deux questions en parallèle : comment Tadashi fait des mathématiques (j’espère que j’ai bien compris ! Tadashi fait à la fois de la physique et des mathématiques. Les mathématiciens souvent sont très fiers d’être précis. Par contre les physiciens se disent souvent fiers d’être imprécis et donc créatifs. Pour son premier cours, Tadashi a choisi une chambre dans un château où il n’y avait aucune table.
Tard le soir, après le dessert, on reste à table à discuter. Pourquoi est-il impossible d’attraper un billet avec deux doigts. 3,712 | 30/05/2016 | Traduire: Tadashi Tokieda professeur de l’Université de Cambridge, Il explique pourquoi il est impossible d'attraper quelqu'un un projet de loi de 20 $ en chute libre avec ses doigts.
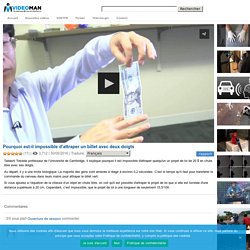
Au départ, il y a une limite biologique: La majorité des gens sont amenés à réagir à environ 0,2 secondes. C’est le temps qu’il faut pour transférer la commande du cerveau dans leurs mains pour attraper le billet vert. Si vous ajoutez à l’équation de la vitesse d’un objet en chute libre, on voit qu'il est possible d'attraper le projet de loi que si elle est tombée d'une distance supérieure à 20 cm. Cependant, c’est impossible, que le projet de loi a une longueur de seulement 15,5/100. Les dés de Condorcet (vus par Tokieda) Jeudi matin, l'association Animath organisait un atelier pour vulgarisateurs scientifiques, tenu par Tadashi Tokieda (University of Cambridge).
Cet atelier de haute tenue faisait suite à la conférence donnée par Tokieda la veille à la BnF pour le cycle "Un texte, un mathématicien" (le texte était ... une feuille de papier à partir de laquelle Tokieda a fait des origamis). Jeudi matin, Tokieda a donné de nombreux exemples fort intéressants. Arrêtons-nous sur celui des dés. Wikipedia (auteur aney) appelle cela... un dé japonais ! Soient quatre dés anormaux : - le dé A : 3 sur les 6 faces. - le dé B : 4 sur 4 faces, 0 sur 2 faces. - le dé C : 5 sur 3 faces, 1 sur 3 faces. - le dé D : 6 sur 2 faces, 2 sur 4 faces. On cherche à classer les dés 2 à 2. Dr Tadashi Tokieda, mathématicien très joueur!