

Quadruple-precision floating-point format. In computing, quadruple precision (also commonly shortened to quad precision) is a binary floating-point-based computer number format that occupies 16 bytes (128 bits) in computer memory and whose precision is about twice the 53-bit double precision.
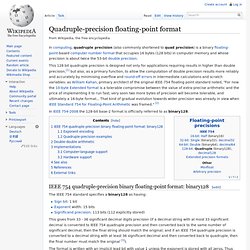
This 128 bit quadruple precision is designed not only for applications requiring results in higher than double precision,[1] but also, as a primary function, to allow the computation of double precision results more reliably and accurately by minimising overflow and round-off errors in intermediate calculations and scratch variables: as William Kahan, primary architect of the original IEEE-754 floating point standard noted, "For now the 10-byte Extended format is a tolerable compromise between the value of extra-precise arithmetic and the price of implementing it to run fast; very soon two more bytes of precision will become tolerable, and ultimately a 16-byte format... The IEEE 754 standard specifies a binary128 as having: ). See also[edit] IEEE Standard 754 Floating-Point. Steve Hollasch / Last update 2005-Feb-24 IEEE Standard 754 floating point is the most common representation today for real numbers on computers, including Intel-based PC's, Macintoshes, and most Unix platforms.

This article gives a brief overview of IEEE floating point and its representation. Discussion of arithmetic implementation may be found in the book mentioned at the bottom of this article. What Are Floating Point Numbers? There are several ways to represent real numbers on computers. Floating-point representation - the most common solution - basically represents reals in scientific notation. Floating-point solves a number of representation problems.
Floating-point, on the other hand, employs a sort of "sliding window" of precision appropriate to the scale of the number. Storage Layout IEEE floating point numbers have three basic components: the sign, the exponent, and the mantissa. Fraction and an implicit leading digit (explained below). A Level Computing OCR exam board - Normalised Floating Point. We want the floating point system to represent as wide a range of real numbers with as much precision as possible.
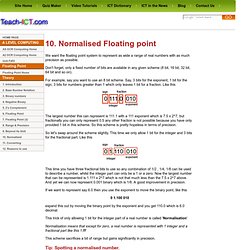
Don't forget, only a fixed number of bits are available in any given scheme (8 bit, 16 bit, 32 bit, 64 bit and so on). For example, say you want to use an 8 bit scheme. Say, 3 bits for the exponent, 1 bit for the sign, 3 bits for numbers greater than 1 which only leaves 1 bit for a fraction. Like this The largest number this can represent is 111.1 with a 111 exponent which is 7.5 x 2^7, but fractionally you can only represent 0.5 any other fraction is not possible because you have only provided 1 bit in this scheme.
So let's swap around the scheme slightly. This time you have three fractional bits to use so any combination of 1/2 , 1/4, 1/8 can be used to describe a number, whilst the integer part can only be a 1 or a zero. If we want to represent say 6.0 then you use the exponent to move the binary point, like this. C# in Depth: Binary floating point in .NET. Lots of people are at first surprised when some of their arithmetic comes out "wrong" in .NET.

This isn't something specific to .NET in particular - most languages/platforms use something called "floating point" arithmetic for representing non-integer numbers. This is fine in itself, but you need to be a bit aware of what's going on under the covers, otherwise you'll be surprised at some of the results. It's worth noting that I am not an expert on this matter. Since writing this article, I've found another one - this time written by someone who really is an expert, Jeffrey Sax. Tutorial: Floating-Point Binary. The two most common floating-point binary storage formats used by Intel processors were created for Intel and later standardized by the IEEE organization: Both formats use essentially the same method for storing floating-point binary numbers, so we will use the Short Real as an example in this tutorial.

The bits in an IEEE Short Real are arranged as follows, with the most significant bit (MSB) on the left: The Sign. Floating point. A diagram showing a representation of a decimal floating-point number using a mantissa and an exponent.
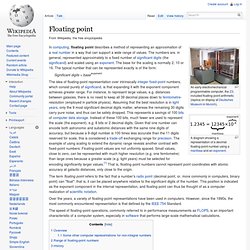
In computing, floating point describes a method of representing an approximation of a real number in a way that can support a wide range of values. The numbers are, in general, represented approximately to a fixed number of significant digits (the significand) and scaled using an exponent. The base for the scaling is normally 2, 10 or 16. The typical number that can be represented exactly is of the form: Significant digits × baseexponent The term floating point refers to the fact that a number's radix point (decimal point, or, more commonly in computers, binary point) can "float"; that is, it can be placed anywhere relative to the significant digits of the number. A Level Computing OCR exam board - Normalised Floating Point. Double-precision floating-point format. Tutorial: Floating-Point Binary.