

Www.ostralo.net : Animations en physique. Activité commentée sur la notion de référentiel ostralo net. Mouvement - Simulations PhET.
Jeux de révisions 6ème. Carte mentale commune au cycle 4. P2C4 4e Carac mvt 2016 2017 v2. Version corrigée. Coccinelle en mouvement 2D - Position, Vitesse, Accélération. Savoir convertir des unités de vitesse km/h vers m/s. Le mouvement cycle 3 (rappels donc!) P2C4 4e TP rail (tablette) En route vers la 3ème. P2C4 4e rappels3e. Choix du Référentiel. Chute d’un objet du haut du mât d’un navire. La relativité galliléenne. P2C4 3e Fiche d'activité. TP rétrogradation Mars. Rétrogradation de Mars - Date pour Winstar. La rétrogradation de Mars. Comment tracer la trajectoire.
Rétrogradation de Mars - tracé d'élève. Trajectoires des astres dans le systéme géocentrique. Centered on This simulation shows the four inner planets of the solar system, as they orbit the Sun.

Moving out from the Sun, we see Mercury, Venus, Earth, and Mars, in that order. The strip at the bottom shows what the other four objects look like in the sky, as viewed from an observer on whatever object is at the center. Note that there are various scales in the picture. The relative sizes of the planets (and, in the strip at the bottom, their relative apparent sizes) are approximately correct. On March 12, 2019, Physics Today published a commentary by Tom Stockman, Gabriel Monroe, and Samuel Cordner, that looked at which planet was the nearest neighbor to Earth. This simulation allows an exploration of this idea, and the simulation tracks the distance at any time, as well the average distance. This work by Andrew Duffy is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.This simulation can be found in the collection at.
Copernic et Galilée. Référentiel. Cette vidéo représente bien la notion de point de vue que l'on appelle en physique : le référentiel.

Pour décrire un mouvement il est donc essentiel de bien spécifier le référentiel, car sinon la description peut être fausse. Prenons l'exemple d'une balle que l'on lâche dans un train en mouvement. Lorsque l'on lâche la balle, si on se place dans le référentiel du train (le point de vue du train), la balle rebondie de manière rectiligne. Mais hors du train, dans le référentiel terrestre (point de vue à la surface de la Terre), la balle rebondie selon une trajectoire curviligne. Ainsi tous les mouvement que l'on observe sont lié à notre point de vue. Si on change de référentiel (de point de vue), que l'on se place au centre du Soleil : c'est le réferentiel héliocentrique, ce sont en fait les planètes et la Terre qui tourne autour du Soleil.
On peut pousser plus loin encore en tenant compte du mouvement du Soleil autour du centre de notre galaxie (la voie lactée). TS Cours chapitre 12 - Alpha Scorpii. Epicycles de Ptolémée (animation) Epicycles de Ptolémée Pour les grecs depuis Aristote (−385, −322) la Terre était le centre du Monde.
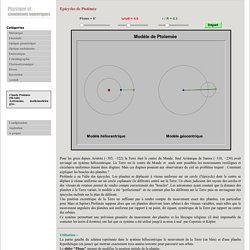
Seul Aristarque de Samos (−310, −230) avait envisagé un système héliocentrique. La Terre est le centre du Monde et seuls sont possibles les mouvements rectilignes et circulaires uniformes étaient deux dogmes. Mais ces dogmes posaient aux observateurs du ciel un problème majeur : Comment expliquer les boucles des planètes ? Ptolémée a eu l'idée des épicycles. Utilisation : La partie gauche du schéma représente dans le système héliocentrique le mouvement de la Terre (en bleu) et d'une planète hypothétique (en jaune) qui mettrait exactement trois années terrestre pour parcourir son orbite. Le slider rouge permet de modifier le rapport des vitesses de rotation entre l'épicycle et le déférent.
Le slider vert permet de modifier le rayon de l'épicycle. Le bouton [Départ] permet de lancer l'animation la pause et la reprise de l'animation.. Les Mathématiques de la Relativité Générale.