

What's a Tensor? Mises Criterion & Tresca Criterion - FailureCriteria.com. How Do Mises and Tresca Fit In All mechanics of materials books have sections on strength and failure criteria.

Usually the Mises and Tresca criteria are presented jointly with little discrimination or recommendation between them. What is more, often little else in the way of failure criteria are presented and the non-expert reader can be left with the impression that these two criteria cover all or nearly all materials, and it doesn’t greatly matter which one is used. Some books even grant these two criteria the status of being classical results. A general question to be posed here is this, can either or both of these criteria be considered to be classical results or are they merely long standing, comfortable forms but of no special distinction.
This website has made several references to the Mises criterion while the Tresca criterion has barely been mentioned. The two criteria are specified below in principal stress space. Mises Criterion, Critical Distortional Energy where. Hooke's law. Hooke's law: the force is proportional to the extension Manometers are based on Hooke's law.
The force created by gas pressure inside the coiled metal tube at right unwinds it by an amount proportional to the pressure. The balance wheel at the core of many mechanical clocks and watches depends on Hooke's law. Since the torque generated by the coiled spring is proportional to the angle turned by the wheel, its oscillations have a nearly constant period. Hooke's law is a principle of physics that states that the force is proportional to that distance. Where. Graphics Systems' SolidNotes: FEA & Design Analysis. Pop quiz!
Name the following items: and OK, let's see how well you did. A. = Accelerometers B. = Pitot Tube C. = Strain Gauges D. = Thermocouple E. = Eyedroppers You probably see the commonality in all of these items, no? Plasticity (physics) "Plastic material" redirects here.
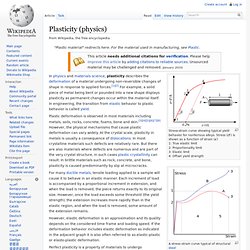
For the material used in manufacturing, see Plastic. Stress-strain curve showing typical yield behavior for nonferrous alloys. Linear elasticity. Mathematical formulation[edit] Direct tensor form[edit] In direct tensor form that is independent of the choice of coordinate system, these governing equations are:[1] Equation of motion, which is an expression of Newton's second law: Constitutive equations.
Elasticidad (mecánica de sólidos) Una varilla elástica vibrando, es un ejemplo de sistema donde la energía potencial elástica se transforma en energía cinética y viceversa.
En física el término elasticidad designa la propiedad mecánica de ciertos materiales de sufrir deformaciones reversibles cuando se encuentran sujetos a la acción de fuerzas exteriores y de recuperar la forma original si estas fuerzas exteriores se eliminan. La elasticidad es estudiada por la teoría de la elasticidad, que a su vez es parte de la mecánica de sólidos deformables. La teoría de la elasticidad (ETE) como la mecánica de sólidos (MS) deformables describe cómo un sólido (o fluido totalmente confinado) se mueve y deforma como respuesta a fuerzas exteriores. La diferencia entre la TE y la MS es que la primera sólo trata sólidos en que las deformaciones son termodinámicamente reversibles y en los que el estado tensiones en un punto en un instante dado dependen sólo de las deformaciones. Young's modulus. Von Mises Yield Criterion demystified. Everybody uses Von Mises Yield Criterion without knowing what exactly it is.

Mohr's circle. Figure 1.
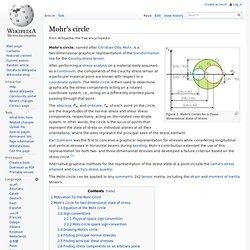
Mohr's circles for a three-dimensional state of stress Mohr's circle, named after Christian Otto Mohr, is a two-dimensional graphical representation of the transformation law for the Cauchy stress tensor. After performing a stress analysis on a material body assumed as a continuum, the components of the Cauchy stress tensor at a particular material point are known with respect to a coordinate system.
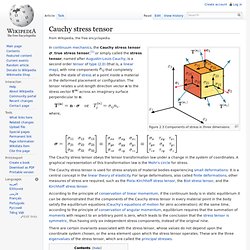
The Mohr circle is then used to determine graphically the stress components acting on a rotated coordinate system, i.e., acting on a differently oriented plane passing through that point. The abscissa, , and ordinate, Cauchy stress tensor. Figure 2.3 Components of stress in three dimensions In continuum mechanics, the Cauchy stress tensor , true stress tensor,[1] or simply called the stress tensor, named after Augustin-Louis Cauchy, is a second order tensor of type (2,0) (that is, a linear map), with nine components where,
Strength of Materials. Mohr's Circle Stress Analysis for 2D & 3D cases. Von Mises Stress ,Yield Criterion & Distortion energy theory. Hydrostatic, Deviatoric Stresses. Introduction Purchase this page for $0.99 Buy optimized PDF files of this webpage that can be read and printed offline, no internet access required.

For $0.99, you receive two optimized PDFs: the first for 8.5" x 11" pages, the second for tablets (iPads, Kindle, etc). This page introduces hydrostatic and deviatoric stresses. The two are subsets of any given stress tensor, which, when added together, give the original stress tensor back. Hydrostatic Stress Hydrostatic stress is simply the average of the three normal stress components of any stress tensor. \sigma_{\text{Hyd}} = {\sigma_{11} + \sigma_{22} + \sigma_{33} \over 3} There are many alternative ways to write this.
\sigma_{\text{Hyd}} \; = \; {1 \over 3} \text{tr}(\boldsymbol{\sigma}) \; = \; {1 \over 3} I_1 \; = \; {1 \over 3} \sigma_{kk} SolidWorks Simulation Professional: Heavy Equipment & Machinery. Von Mises Stress ,Yield Criterion & Distortion energy theory. Continuum Mechanics. Continuum mechanics. From Wikipedia, the free encyclopedia Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modeled as a continuum. The French mathematician Augustin Louis Cauchy was the first to formulate such models in the 19th century, but research in the area continues today. Modeling an object as a continuum assumes that the substance of the object completely fills the space it occupies. Modeling objects in this way ignores the fact that matter is made of atoms, and so is not continuous; however, on length scales much greater than that of inter-atomic distances, such models are highly accurate.
Random vibration. Von Mises Criterion ( Maximum Distortion Energy Criterion ) - Strength (Mechanics ) of Materials. Strength / Mechanics of Materials Table of Contents This criterion is based on the determination of the distortion energy in a given material, i.e., of the energy associated with changes in the shape in that material( as opposed to the energy associated with the changes in volume in the same material. According to this criterion, named after German-American applied mathematician Richard von Mises (1883-1953), a given structural material is safe as long as the maximum value of the distortion energy per unit volume in that material remains smaller than the distortion energy per unit volume required to cause yield in a tensile-test specified of the same material.
Mathematically the yield function for the von Mises condition is expressed as: What are von mises stresses exactly in laymans language? Good question. Von Mises Stress is actually a misnomer. It refers to a theory called the "Von Mises - Hencky criterion for ductile failure". In an elastic body that is subject to a system of loads in 3 dimensions, a complex 3 dimensional system of stresses is developed (as you might imagine). That is, at any point within the body there are stresses acting in different directions, and the direction and magnitude of stresses changes from point to point. SolidWorks Simulation Failure Mode Analysis: Vibration. Webinar SolidWorks Simulation - Frequency Analysis - Frequency Analysis: Wat, wanneer en waarom?
Fatigue Failure Analysis. SolidWorks Video Tutorials: SolidWorks Tutorial: Static Analysis. SolidWorks Video Tutorials: SolidWorks Tutorial: Static Analysis.