

Algorithmes. Claire Mathieu est Directrice de Recherche au Centre National de la Recherche Scientifique.
Elle travaille au Département d’Informatique de L’École Normale Supérieure et à l’Irif, Université Paris-Diderot. Elle est la toute nouvelle titulaire de la Chaire « Informatique et sciences numériques » du Collège de France où elle présente un cours intitulé « Algorithmes » (leçon inaugurale le 16 novembre 2017). Les algorithmes fascinent, peuvent inquiéter, prennent une place considérable dans nos vies.
Il nous faut mieux les comprendre pour qu’ils fassent ce que nous voulons. Entrons avec Claire Mathieu, parmi les meilleurs spécialistes mondiaux du domaine, dans leur monde merveilleux . Claire est également une éditrice invitée fidèle de Binaire. Claire Mathieu Les algorithmes, quand ils sont bien conçus car bien compris, contribuent au bien social et sont un outil de transformation de la société. Portail:Algorithmique. Une page de Wikipédia, l'encyclopédie libre.
Portail Algorithmique On désigne par algorithmique l’ensemble des activités logiques qui relèvent des algorithmes ; en particulier, en informatique, cette discipline désigne l'ensemble des règles et des techniques qui sont impliquées dans la définition et la conception des algorithmes. Le mot vient du nom du mathématicien Al-Khuwarizmi (latinisé au Moyen Âge en Algoritmi), qui, au IXe siècle écrivit le premier ouvrage systématique sur la solution des équations linéaires et quadratiques.
L'informatique théorique : un domaine foisonnant, malgré le blocage persistant de certaines questions fondamentales. Jean-Paul Delahaye, professeur d'Informatique à Lille L'informatique théorique : un domaine foisonnant, malgré le blocage persistant de certaines questions fondamentales Depuis deux décennies, l'informatique a connu une évolution rapide qui a suscité une réflexion théorique d'une extrême richesse.
Comme à chaque fois en de pareilles circonstances, on s'est aperçu que les mathématiques disponibles non seulement ne répondaient pas à toutes les questions qui se posaient, mais qu'en fait, des domaines mathématiques nouveaux devaient être définis et explorés. Référence (informatique) Un article de Wikipédia, l'encyclopédie libre.
En programmation, une référence est une valeur qui permet l'accès en lecture et/ou écriture à une donnée située soit en mémoire principale soit ailleurs. Une référence n'est pas la donnée elle-même mais seulement une information de localisation. La plupart des langages de programmation permettent l'utilisation de références, que ce soit de façon explicite ou implicite. Généralement, les références sont utilisables via des types de données disjoints du type de la donnée référencée (quand le langage dispose d'un système de typage).
Le typage des références permet de manipuler les données référencées de manière abstraite tout en respectant leurs propres contraintes de type. Pointeur (programmation) Un article de Wikipédia, l'encyclopédie libre.
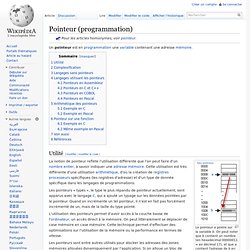
Pour les articles homonymes, voir pointeur. Le pointeur a pointe sur la variable b. On peut noter que b contient un nombre (en hexadécimal 00000011 = en décimal 17), et que a contient l'adresse de b en mémoire (en hexadécimal 1008). Dans ce cas précis, l'adresse et la donnée sont contenues dans 32 bits. L'utilisation des pointeurs permet d'avoir accès à la couche basse de l'ordinateur, un accès direct à la mémoire. Les pointeurs sont entre autres utilisés pour stocker les adresses des zones mémoires allouées dynamiquement par l'application.
Graphes et arbres. Arbre binaire. Un article de Wikipédia, l'encyclopédie libre.
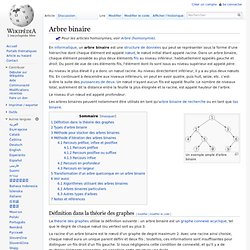
Au niveau le plus élevé il y a donc un nœud racine. Au niveau directement inférieur, il y a au plus deux nœuds fils. En continuant à descendre aux niveaux inférieurs, on peut en avoir quatre, puis huit, seize, etc. c'est-à-dire la suite des puissances de deux. Tas (informatique) Un article de Wikipédia, l'encyclopédie libre.
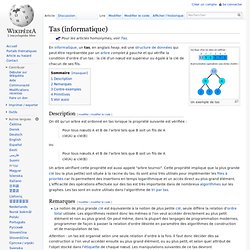
Pour les articles homonymes, voir Tas. Un exemple de tas En informatique, un tas, en anglais heap, est une structure de données qui peut-être représentée par un arbre complet à gauche et qui vérifie la condition d'ordre d'un tas : la clé d'un nœud est supérieur ou égale à la clé de chacun de ses fils. On dit qu'un arbre est ordonné en tas lorsque la propriété suivante est vérifiée : Pour tous nœuds A et B de l'arbre tels que B soit un fils de A clé(A) ≥ clé(B) ou. Tas binaire. Un article de Wikipédia, l'encyclopédie libre.
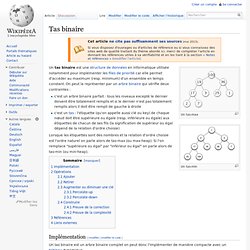
Un tas-max Un tas-min. Arbre enraciné. Un article de Wikipédia, l'encyclopédie libre.
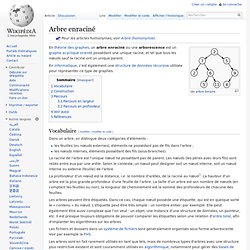
En théorie des graphes, un arbre enraciné ou une arborescence est un graphe acyclique orienté possédant une unique racine, et tel que tous les nœuds sauf la racine ont un unique parent. En informatique, c'est également une structure de données récursive utilisée pour représenter ce type de graphes. Vocabulaire[modifier | modifier le code]
Induction. Calculabilité. Un article de Wikipédia, l'encyclopédie libre.
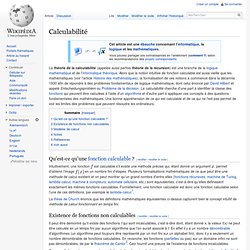
Qu'est-ce qu'une fonction calculable ? [modifier | modifier le code] Intuitivement, une fonction. Récursivité. Un article de Wikipédia, l'encyclopédie libre.
La récursivité est une démarche qui fait référence à l'objet de la démarche. Ainsi, les cas suivants constituent des cas concrets de récursivité : Décrire un processus dépendant de données en faisant appel à ce même processus sur d'autres données plus « simples » ;Montrer une image contenant des images similaires[1]Définir un concept en invoquant le même conceptÉcrire un algorithme qui s'invoque lui-même[2].
Récursivité en informatique et en logique[modifier | modifier le code] Fonction récursive. Un article de Wikipédia, l'encyclopédie libre. Sur les autres projets Wikimedia : récursif, sur le Wiktionnaire. Fonction récursive primitive. Un article de Wikipédia, l'encyclopédie libre. Définition d'une fonction récursive primitive[modifier | modifier le code] On s'intéresse aux fonctions définies sur l'ensemble des entiers naturels, ou sur les ensembles des -uplets d'entiers naturels, et à valeurs dans On construit les fonctions récursives primitives de proche en proche en partant des trois fonctions de base : Fonction d'Ackermann.
Un article de Wikipédia, l'encyclopédie libre. Dans la théorie de la récursivité, la fonction d'Ackermann (aussi appelée fonction d'Ackermann-Péter) est un exemple simple de fonction récursive non récursive primitive, trouvée en 1926 par Wilhelm Ackermann. Elle est souvent présentée sous la forme qu'en a proposé la mathématicienne Rózsa Péter, comme une fonction à deux paramètres entiers naturels comme arguments et qui retourne un entier naturel comme valeur, noté en général A(n, m).
Histoire[modifier | modifier le code] Dans les années 1920, Wilhelm Ackermann et Gabriel Sudan, alors étudiants sous la direction de David Hilbert, étudiaient les fondements de la calculabilité. Fonction de Sudan. Un article de Wikipédia, l'encyclopédie libre. En calculabilité, la fonction de Sudan est un exemple de fonction récursive mais non récursive primitive. C'est aussi le cas de la bien plus connue fonction d'Ackermann. Elle fut conçue en 1927 par le mathématicien roumain Gabriel Sudan, élève de David Hilbert.
Définition[modifier | modifier le code] Algorithme récursif. Récursivité structurelle. Acronymie récursive. Autonymie. Récursion terminale. Récursion mutuelle. Évaluation paresseuse. Théorème de récursion de Kleene. Récursivité gauche. Operational semantics. The operational semantics for a programming language describes how a valid program is interpreted as sequences of computational steps. These sequences then are the meaning of the program. In the context of functional programs, the final step in a terminating sequence returns the value of the program. (In general there can be many return values for a single program, because the program could be nondeterministic, and even for a deterministic program there can be many computation sequences since the semantics may not specify exactly what sequence of operations arrives at that value.)
The concept of operational semantics was used for the first time in defining the semantics of Algol 68. Imprédicativité. Réflexion (informatique) Quine (informatique) Autopoïèse. Énaction. Dixième problème de Hilbert. Thèse de Church. Thèse de Church-Turing.pdf. Discussion:Thèse de Church. Déterminisme (calculabilité) Hypercalcul. Calculateur quantique. Oméga de Chaitin. Problème de l'arrêt. Turing - On computable numbers... Algorithms, equivalence of. Calculabilité, langages formels, Algorithmes, Automates.
Calcul formel. Langage formel. Système de calcul formel. Monoïde. Logique combinatoire. Logique combinatoire. Ontologie (informatique) Complexités : des mathématiques, de la logique et de l'informatique - un blog Scilogs.frComplexités. P=NP? Theoretical computer science. Random-access machine.
Model of computation. Semantics (computer science) Denotational semantics. Programming Computable Functions. Node (computer science)