

Chimie quantique. La règle de Walsh. L'opérateur hamiltonien-Les solutions de l'Hamiltonien moléculaire : les orbitales moléculaires. La méthode LCAO.
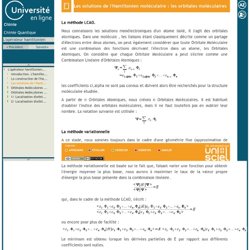
Nous connaissons les solutions monélectroniques d'un atome isolé, il s'agit des orbitales atomiques. Dans une molécule , les liaisons étant classiquement décrite comme un partage d'électrons entre deux atomes, on peut également considérer que toute Orbitale Moléculaire est une combinaison des fonctions décrivant l'électron dans un atome, les Orbitales Atomiques. On considère que chaque Orbitale Moléculaire a peut s'écrire comme une Combinaison Linéaire d'Orbitales Atomiques : les coefficients ci,alpha ne sont pas connus et doivent alors être recherchés pour la structure moléculaire étudiée. A partir de n Orbitales Atomiques, nous créons n Orbitales Moléculaires. La méthode variationnelle A ce stade, nous sommes toujours dans le cadre d'une géométrie fixe (approximation de Born-Oppenheimer). Qui, dans le cadre de la méthode LCAO, s'écrit : ou encore pour plus de facilité : Pour plus de simplicité, dans la suite du développement, on notera :
L'opérateur hamiltonien-La construction de l'Hamiltonien moléculaire et les approximations. Un hamiltonien complet décrivant les particules d'un système moléculaire complexe (plusieurs atomes) peut s'écrire sous la forme simplifiée : avec - T e et T N les expressions décrivant le comportement cinétique des électrons et des noyaux respectivement. - V eN correspond au potentiel attractif ressenti par les électrons placés dans le champ positif des noyaux.

L'opérateur hamiltonien-Introduction. L'hamiltonien Moléculaire - La construction des orbitales moléculaires – Le cadre du modèle. Les Orbitales Moléculaires-Les bases d'orbitales atomiques. Les Orbitales Moléculaires-Introduction : La représentation des Orbitales Atomiques et les Méthodes de résolution de l'équation de Schrödinger. Les deux premiers chapitres nous ont permis de définir la forme des équations et de leurs solutions d'un coté au niveau atomique et de l'autre au niveau moléculaire.
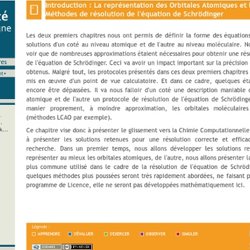
Nous avons pu voir que de nombreuses approximations étaient nécessaires pour obtenir une résolution aisée de l'équation de Schrödinger. Ceci va avoir un impact important sur la précision des résultats obtenus. Malgré tout, les protocoles présentés dans ces deux premiers chapitres doivent être mis en œuvre d'un point de vue calculatoire. Et dans ce cadre, quelques étapes doivent encore être dépassées. Effet inductif et effet mésomère. 2.Effet mésomère La mésomérie désigne le fait que des électrons peuvent se délocaliser sur une ou plusieurs liaisons d'une molécule.
Dans ce contexte, sa représentation de Lewis n'est plus unique mais résulte d'une combinaison de plusieurs structures dites mésomères. Seuls les électrons de type sont concernés par cet effet, qui naît du recouvrement d'orbitales (généralement des orbitales p) avec des orbitales vacantes et/ou des doublets non liants. Une molécule présentant plusieurs formes mésomères est stabilisée. Par exemple le phénol (figure 2) est un système conjugué.
Orbitales Atomiques / Orbitales Moléculaires. Les Orbitales Moléculaires-La Méthode Hatree-Fock. Nous avions défini un Hamiltonien électronique approché : Le corrolaire de cette approximation est alors que la fonction d'onde totale peut-être considérée comme le produit des solutions mono-électroniques de cette équation On écrit : Malheureusement, cette fonction d'onde ne satisfait pas au principe de Pauli qui stipule que la fonction d'onde décrivant un système multiélectronique doit changer de signe lors de la permutation des coordonnées de deux électrons quelconques. Pour obéir au principe de Pauli, il faut introduire une fonction qui permettra de définir les propriétés de spin. L'opérateur hamiltonien-2/ Localisation d'orbitales - Orbitales localisées de BeH2. L'opérateur hamiltonien-1/ Localisation d'orbitales - Orbitales localisées du méthane.
La molécule de méthane, CH 4 , possède une géométrie tétraédrique qui peut être insérée dans un cube, comme présenté dans la figure ci-dessous : L'opérateur hamiltonien-Orbitales Moléculaires d'une molécule diatomique hétéronucléaire. On suppose que les deux noyaux de deux atomes de type différents sont maintenus à une distance fixe (ce qui revient à appliquer l'approximation de Born-Oppenheimer).
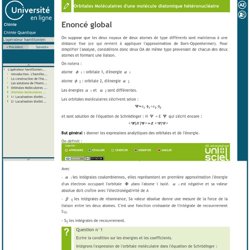
Pour simplifier l'analyse, considérons donc deux OA de même type provenant de chacun des deux atomes et formant une liaison. On notera : atome 1 : orbitale 1, d'énergie. Les Orbitales Atomiques-Les spin-orbitales. L'électron est une particule chargée en mouvement autour du noyau.

Dans ce cadre, il a été démontré que l'électron possède un moment magnétique permanent, qui est appelé moment magnétique orbital. Le mouvement associé de l'électron est appelé mouvement orbital. Lorsque cet électron est placé dans le champ d'une impulsion magnétique, alors un terme supplémentaire décrivant cette origine magnétique doit être ajouté à l'énergie potentielle de l'électron. Les fonctions propres de l'opérateur Hamiltonien que nous avons décrit précédemment, et qui ne comporte pas de terme magnétique, sont encore fonctions propres de ce nouvel opérateur.
Les Orbitales Atomiques-Nomenclature, Nature et Propriétés des solutions obtenues. - Nomenclature : Le nombre quantique n permet de spécifier une couche électronique.
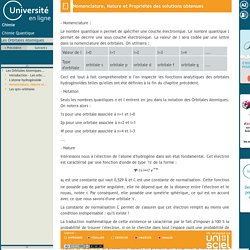
Le nombre quantique l permet de décrire une sous couche électronique. Les Orbitales Atomiques-Nomenclature, Nature et Propriétés des solutions obtenues. Les Orbitales Atomiques-L'atome hydrogénoïde. L'étude de l'atome hydrogénoïde se résume donc à l'étude d'un système dans lequel deux particules sont présentes : - un noyau de masse M et de charge +Ze - un électron de masse me et de charge -e L'équation de Schrödinger indépendante du temps s'écrit : Afin de simplifier cette équation, on se ramène au centre de masse du système.
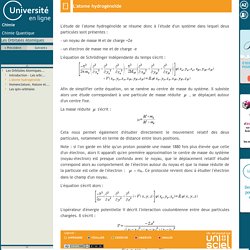
Il subsiste alors une étude correspondant à une particule de masse réduite , se déplaçant autour d'un centre fixe. La théorie des Orbitales Moléculaires. Chapitre 1 Introduction. « Perhaps life is a characteristic of matter, and man is the agent whose part in a cycle of the universe is to break up old worlds and to make them into new. »

Chimie quantique. La chimie quantique utilise les résultats de la mécanique quantique pour interpréter des phénomènes chimiques, comme la liaison chimique sous la forme de diagrammes d'orbitales moléculaires, la réactivité chimique des molécules ainsi que les mécanismes réactionnels.

La mécanique quantique sert avant tout à décrire le comportement des particules élémentaires. En chimie, on s'intéressera essentiellement à la description des électrons. La base de la mécanique quantique repose sur un certain nombre de postulats plus apparentés aux mathématiques qu'à la physique traditionnelle. Chimie quantique. La chimie est la science qui étudie la nature et les propriétés des corps simples, l'action moléculaire de ces corps les uns sur les autres et les combinaisons dues à cette action.

(Larousse) Dernière mise à jour de ce chapitre: 2014-04-06 20:42:41 | {oUUID 1.721} Version: 3.2 Révision 11 | Rédacteur: Vincent ISOZ | Avancement: ~90% vues depuis le 2012-01-01: 0 Avant que le lecteur aille plus loin dans la lecture de cette section du site, nous souhaitons rappeler que le site traite de mathématique appliquée et de physique théorique. Ainsi, nous traiterons dans cette section uniquement de chimie théorique (chimique quantique théorique, thermochimie théorique, chimie cinétique théorique, ...). Ce choix fait suite à l'évolution du visage de la chimie ces vingt dernières décennies: de science en grande partie descriptive, elle tend à devenir déductive. Nous allons considérer maintenant une particule se mouvant librement dans la boîte tridimensionnelle ci-dessous. Introduction à la chimie quantique. Chimie quantique - Simulations PhET. Chimie quantique. Bands diagram using VASP and pymatgen Lundi 7 avril 2014 This article presents a python source code in order to plot the bands diagram of graphene calculated using VASP.
The plot is done using pymatgen library and RGB coloring adapted from this example. Here is the output obtained with the script : On the band diagram, the contribution of s, (px,py) and pz atomic orbital […] Outils pour la symétrie moléculaire : théorie des groupes Samedi 9 juin 2012 En chimie et en physique, on utilise les propriétés de symétrie du système pour simplifier la résolution. Vasptools : a package for vasp post treatments Mercredi 25 avril 2012 vasptools is a package wrote in python in order to do pre or post treatments of a VASP calculations. Guide pour tracer des graphiques en coordonnées polaires ou sphériques Mercredi 11 janvier 2012 Orbites de l’atome de Bohr Lundi 9 janvier 2012 Niels Bohr (1885 – 1962) était un physicien danois.
Transitions électroniques.