

Dimensions Home. A film for a wide audience!
Nine chapters, two hours of maths, that take you gradually up to the fourth dimension. Mathematical vertigo guaranteed! Background information on every chapter: see "Details". Click on the image on the left to watch the trailer ! (turn your speakers on please). Free download and you can watch the films online! The film can also be ordered as a DVD.
This film is being distributed under a Creative Commons license. Now with even more languages for the commentary and subtitles: Commentary in Arabic, English, French, German, Italian, Japanese, Spanish and Russian. Abel-Ruffini Theorem. A general solution to any quadratic equation can be given using the quadratic formula, above.
Similar formulas exist for polynomial equations of degree 3 and 4. But no such formula is possible for 5th degree polynomials; the real solution -1.1673... to the 5th degree equation above cannot be written using basic arithmetic operations and nth roots. In algebra, the Abel–Ruffini theorem (also known as Abel's impossibility theorem) states that there is no general algebraic solution—that is, solution in radicals— to polynomial equations of degree five or higher.[1] The theorem is named after Paolo Ruffini, who made an incomplete proof in 1799, and Niels Henrik Abel, who provided a proof in 1823.
Évariste Galois independently proved the theorem in a work that was posthumously published in 1846.[2] Interpretation[edit] The theorem does not assert that higher-degree polynomial equations have no solution. Hausdorff dimension. In mathematics, the Hausdorff dimension (also known as the Hausdorff–Besicovitch dimension) is an extended non-negative real number associated with any metric space.
Topological Dimension. In mathematics, the Lebesgue covering dimension or topological dimension of a topological space is one of several different ways of defining the dimension of the space in a topologically invariant way.
Definition[edit] As a special case, a topological space is zero-dimensional with respect to the covering dimension if every open cover of the space has a refinement consisting of disjoint open sets so that any point in the space is contained in exactly one open set of this refinement. Examples[edit] More generally, the n-dimensional Euclidean space has covering dimension n. Analytic function. Ω-consistent theory. Definition[edit] A theory T is said to interpret the language of arithmetic if there is a translation of formulas of arithmetic into the language of T so that T is able to prove the basic axioms of the natural numbers under this translation.
A T that interprets arithmetic is ω-inconsistent if, for some property P of natural numbers (defined by a formula in the language of T), T proves P(0), P(1), P(2), and so on (that is, for every standard natural number n, T proves that P(n) holds), but T also proves that there is some (necessarily nonstandard) natural number n such that P(n) fails. This may not lead directly to an outright contradiction, because T may not be able to prove for any specific value of n that P(n) fails, only that there is such an n. T is ω-consistent if it is not ω-inconsistent. Primitive Recursion. Every primitive recursive function is a general recursive function.
Definition[edit] The primitive recursive functions are among the number-theoretic functions, which are functions from the natural numbers (nonnegative integers) {0, 1, 2, ...} to the natural numbers. These functions take n arguments for some natural number n and are called n-ary. The basic primitive recursive functions are given by these axioms: Constant function: The 0-ary constant function 0 is primitive recursive.Successor function: The 1-ary successor function S, which returns the successor of its argument (see Peano postulates), is primitive recursive.
Composition: Given f, a k-ary primitive recursive function, and k m-ary primitive recursive functions g1,... The primitive recursive functions are the basic functions and those obtained from the basic functions by applying these operations a finite number of times. Closure (mathematics) Similarly, a set is said to be closed under a collection of operations if it is closed under each of the operations individually.
A set that is closed under an operation or collection of operations is said to satisfy a closure property. Often a closure property is introduced as an axiom, which is then usually called the axiom of closure. Modern set-theoretic definitions usually define operations as maps between sets, so adding closure to a structure as an axiom is superfluous; however in practice operations are often defined initially on a superset of the set in question and a closure proof is required to establish that the operation applied to pairs from that set only produces members of that set. Autonomous system (mathematics)
In mathematics, an autonomous system or autonomous differential equation is a system of ordinary differential equations which does not explicitly depend on the independent variable.
When the variable is time, they are also called time-invariant systems. Many laws in physics, where the independent variable is usually assumed to be time, are expressed as autonomous systems because it is assumed the laws of nature which hold now are identical to those for any point in the past or future. Autonomous systems are closely related to dynamical systems. Any autonomous system can be transformed into a dynamical system and, using very weak assumptions, a dynamical system can be transformed into an autonomous system. Complete metric space. In mathematical analysis, a metric space M is called complete (or a Cauchy space) if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M.
Intuitively, a space is complete if there are no "points missing" from it (inside or at the boundary). For instance, the set of rational numbers is not complete, because e.g. √2 is "missing" from it, even though one can construct a Cauchy sequence of rational numbers that converges to it. (See the examples below.) It is always possible to "fill all the holes", leading to the completion of a given space, as explained below. Supremum. A set A of real numbers (blue balls), a set of upper bounds of A (red diamond and balls), and the smallest such upper bound, that is, the supremum of A (red diamond).
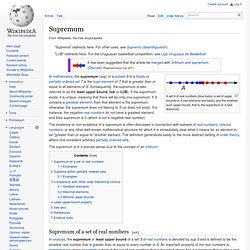
In mathematics, the supremum (sup) of a subset S of a totally or partially ordered set T is the least element of T that is greater than or equal to all elements of S. Consequently, the supremum is also referred to as the least upper bound (lub or LUB). If the supremum exists, it is unique, meaning that there will be only one supremum. If S contains a greatest element, then that element is the supremum; otherwise, the supremum does not belong to S (or does not exist). Table of mathematical symbols. When reading the list, it is important to recognize that a mathematical concept is independent of the symbol chosen to represent it.
For many of the symbols below, the symbol is usually synonymous with the corresponding concept (ultimately an arbitrary choice made as a result of the cumulative history of mathematics), but in some situations a different convention may be used. For example, depending on context, the triple bar "≡" may represent congruence or a definition. Further, in mathematical logic, numerical equality is sometimes represented by "≡" instead of "=", with the latter representing equality of well-formed formulas. In short, convention dictates the meaning. Each symbol is shown both in HTML, whose display depends on the browser's access to an appropriate font installed on the particular device, and in TeX, as an image. Guide[edit] This list is organized by symbol type and is intended to facilitate finding an unfamiliar symbol by its visual appearance. Philosophy of Mathematics. First published Tue Sep 25, 2007; substantive revision Wed May 2, 2012.
List of important publications in mathematics. Topological space. Definition[edit] Neighbourhoods definition[edit] The first three axioms for neighbourhoods have a clear meaning. Function space. Examples[edit] Function spaces appear in various areas of mathematics: Functional analysis[edit] Functional analysis is organized around adequate techniques to bring function spaces as topological vector spaces within reach of the ideas that would apply to normed spaces of finite dimension. Bibliography[edit] Kolmogorov, A. Peano axioms. Continuum hypothesis. This article is about the hypothesis in set theory. For the assumption in fluid mechanics, see Fluid mechanics. Comparison of vector algebra and geometric algebra. Vector algebra and geometric algebra are alternative approaches to providing additional algebraic structures on vector spaces, with geometric interpretations, particularly vector fields in multivariable calculus and applications in mathematical physics.
Vector algebra is specific to Euclidean 3-space, while geometric algebra uses multilinear algebra and applies in all dimensions and signatures, notably 3+1 spacetime as well as 2 dimensions. They are mathematically equivalent in 3 dimensions, though the approaches differ. List of vector identities. Operator notations[edit] Metric space. Greek letters used in mathematics, science, and engineering.