

Бутузов В.Ф. и др. Математический анализ в вопросах и задачах: Учеб. пособие. Разложение в ряд Маклорена. Математика на cleverstudents (ru) - теория, примеры, решения. Математический портал. Практические занятия по высшей математике. Замечательные пределы. Примеры решений. Продолжаем наш разговор на тему Пределы и способы их решения.
Перед изучением материалов данной страницы настоятельно рекомендую ознакомиться со статьей Пределы. Примеры решений. Из вышеуказанной статьи Вы сможете узнать, что же такое предел, и с чем его едят – это ОЧЕНЬ важно. Почему? Можно не понимать, что такое определители и успешно их решать, можно совершенно не понимать, что такое производная и находить их на «пятёрку». А для целей данного урока нам потребуются следующие методические материалы: Замечательные пределы и Тригонометрические формулы.
Чем же замечательны замечательные пределы? Замечательных пределов существует несколько, но на практике у студентов-заочников в 95% случаев фигурируют два замечательных предела: Первый замечательный предел, Второй замечательный предел. Начнем. Первый замечательный предел Рассмотрим следующий предел: (вместо родной буквы «хэ» я буду использовать греческую букву «альфа», это удобнее с точки зрения подачи материала). ! Примеры: Здесь Почему? ? ». Второй замечательный предел. Примеры решения.
Обычно второй замечательный предел записывают в такой форме: Число , указанное в правой части равенства (1), является иррациональным.
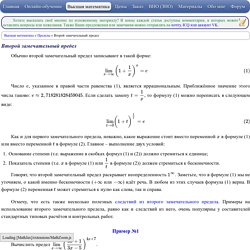
Приближённое значение этого числа таково: . Если сделать замену , то формулу (1) можно переписать в следующем виде: Как и для первого замечательного предела, неважно, какое выражение стоит вместо переменной в формуле (1) или вместо переменной в формуле (2). Главное – выполнение двух условий: Основание степени (т.е. выражение в скобках формул (1) и (2)) должно стремиться к единице;Показатель степени (т.е. в формуле (1) или в формуле (2)) должен стремиться к бесконечности. Говорят, что второй замечательный предел раскрывает неопределенность . Отмечу, что есть также несколько полезных следствий из второго замечательного предела. Jsredir?from=yandex.ru;yandsearch;web;;&text=&etext=941.EPw8ZfWG-UgmX5TCdsqBsoKpcstkMWmSTrDHY8HhQX4.7166a69f9f30df233c225a9fc017935385d5e32e&uuid=&state=PEtFfuTeVD4jaxywoSUvtNlVVIL6S3yQ0eL-KRksnRFetzHgl8sU5u5XKwtZDO6p&data=UlNrNmk5WktYejR0eWJFYk1LdmtxaUV5. Вы пытаетесь перейти по ссылке, которая устарела или ведёт на сайт, угрожающий безопасности компьютера.
Если вы попали сюда из результатов поиска Яндекса: Вернитесь назад и обновите страницу — нажмите клавишу F5.Или введите новый поисковый запрос Если вы попали сюда не из поиска Яндекса: Перед переходом внимательно проверьте адрес ссылки: что адрес правильный (а не просто похож) или получен из достоверного источника. Ссылка может относиться к мошенническому сайту, созданному для фишинга Всё равно перейти: Онлайн калькуляторы по математике, теории вероятности и геометрии. Образовательные онлайн сервисы Главная Математические онлайн калькуляторы Онлайн калькуляторы - это автоматические программы для решения примеров по математике, теории вероятности, физике и геометрии.

Для использования онлайн калькуляторов Вам не надо ничего устанавливать на свой компьютер, Вам надо только ввести данные, дальше программа все сделает сама! Все программы на сайте абсолютно БЕСПЛАТНЫЕ !!! Если вы не хотите вникать в материал и хотите получить подробно решенные и хорошо оформленные задания, то для Вас есть специальная услуга - заказ решения! Метод вспомогательных секущих сфер. При определении линии пересечения двух поверхностей вращения, при их особом взаимном расположении, не всегда рационально применять вспомогательные секущие плоскости.

В некоторых случаях применяют метод вспомогательных секущих сфер – концентрических или эксцентрических. Концентрические сферические посредники применяются при определении линии пересечения двух поверхностей вращения с пересекающимися осями. Каждая из этих поверхностей имеет семейство окружностей, являющихся линиями сечения их концентрическими сферами. Применению метода концентрических сфер должно предшествовать такое преобразование чертежа, в результате которого оси обеих поверхностей должны быть расположены параллельно одной и той же плоскости проекций (рис.151) или одна из осей становиться проецирующей прямой, а вторая - линией уровня (рис.152). Оси поверхностей G и Q параллельны фронтальной плоскости проекций и пересекаются в точки А (рис.151).
Точки 1 и 2 линии пересечения построены с помощью сферы радиуса R. 58. Способ замены плоскостей проекций. Методички и книги » Бауманки.НЕТ. Краткий курс тервера - kratkiy-kurs-tervera.rar [9,36 Mb] (cкачиваний: 362) Методичка по ДЗ (матстат) - matstat-dz.rar [5,53 Mb] (cкачиваний: 269)

Библиотека МГТУ им. Н.Э. Баумана. Educate rk1.