

Regolo. Morenaments. Cinderella. News · Blog · Gallery · Download · Flyer (3.3 MB, PDF) · Indra's Pearls · MatheVital If you love somebody… on: Tue 17 of Sep, 2013 [19:51 UTC] Experience Geometry on your desktop and on the web Easily create startling geometric constructions!
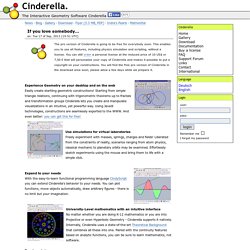
Starting from simple triangle relations, continuing with trigonometric theorems up to fractals and transformation groups Cinderella lets you create and manipulate visualizations in an intuitive, yet powerful way. Using Java® technologies, constructions are seamlessly exported to the WWW. Use simulations for virtual laboratories Freely experiment with masses, springs, charges and fields! Expand to your needs. IMAGINARY. Mathematically, the program visualizes real algebraic geometry in real-time.
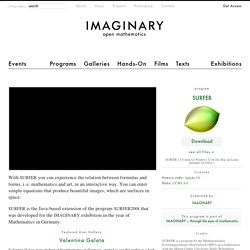
The surfaces shown are given by the zero set of a polynomial equation in the variables x, y and z. 3D-XplorMath Homepage. Geometría no euclidiana. 14 septiembre 2016 por Ana María Teresa Lucca Tal vez fue este deseo de comprensión conceptual lo que hizo a Gauss reacio a publicar, el hecho de que más y más “dudara de la verdad de la geometría”, como él decía.
Pues si hubiera una geometría lógicamente consistente que difiere de la de Euclides sólo porque hace un supuesto diferente sobre el comportamiento de las líneas paralelas, también podría aplicarse al espacio físico, y así la verdad de la geometría (euclidiana) ya no se podría asegurar a priori, como había pensado Kant. Las investigaciones de Gauss sobre la nueva geometría llegaron más lejos de lo que cualquier otra persona pudiera lograr, pero él no las publicó. El honor de ser los primeros en proclamar la existencia de una nueva geometría pertenece a otros dos matemáticos, que lo hicieron a finales de la década de 1820: Nicolay Ivanovich Lobachevsky en Rusia y János Bolyai en Hungría. El árbelos - Geometría - Matemáticas Secundaria (ESO) y Bachillerato.
Leyendo algunos textos de matemáticas en busca de problemas para poner a mis alumnos de secundaria y de bachillerato, me topé con una figura geométrica que ya estaba lejana en mi memoria, pero que me encantó reencontrarme con ella: el árbelos.
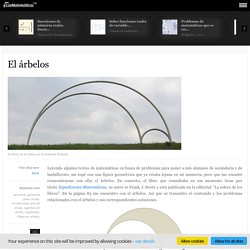
En concreto, el libro que consultaba en ese momento tiene por título Expediciones Matemáticas, su autor es Frank J. Swetz y está publicado en la editorial "La esfera de los libros". En la página 85 me encuentro con el árbelos. Así que os transmito el contenido y los problemas relacionados con el árbelos y sus correspondientes soluciones. En el Libro de Lemmas, Arquímedes introduce una figura que, debido a su forma se conoce históricamente como el "cuchillo de zapatero" o árbelos. Empleo - Documentos y Avisos. GeoGebreando. Los elementos de Euclides. Detalles Categoría: Recursos generales ESO Visitas: 27 Los elementos de Euclides Los Elementos de Euclides es un tratado matemático y geométrico que se compone de trece libros, escrito por el matemático griego Euclides cerca del 300 a.
C. en Alejandría. Recursos de geometría para utilizar en clase o en casa. Recursos de geometría para utilizar en clase o en casa La geometría forma parte de la asignatura de Matemáticas en todas las etapas educativas.
Portales, blogs, plataformas y apps que pueden utilizarse en clase o en casa, siempre con el objetivo de promover el estudio y el repaso de las cuestiones relativas a la geometría para la materia de Matemáticas en Primaria, Secundaria e incluso Bachillerato. Geometría Este portal creado por Enric Puig Amat ofrece información teórica sobre esta rama matemática y permite realizar diferentes figuras, puzzles y también cuenta con una pestaña para autoevaluarse. Jugando y aprendiendo El blog creado por Luisa María Arias que está destinado al alumnado del 5º y 6º de Primaria pone a disposición de docentes y alumnos recursos sobre diferentes materias.
Matemáticas divertidas: Creamos un geoplano humano » Actividades infantil. Ya os presentamos en otra ocasión el recurso del geoplano para trabajar las figuras geométricas con los peques, un material divertido y dinámico con el que se da mucha autonomía a los peques para que vayan construyendo ellos mismos figuras geométricas cambiando de posición las gomas elásticas a su antojo con la ayuda de los clavos del tablero.
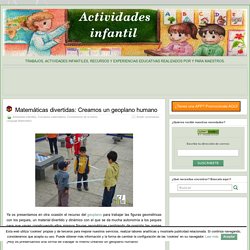
¡Hoy os presentamos una forma de trabajar lo mismo creando un geoplano humano! Para realizar esta actividad necesitamos tener un espacio amplio para que los peques se coloquen en pequeños grupos repartidos por el espacio y unas cintas elásticas. Depende de cuántos peques haya en cada grupo, se podrán hacer una figura geométrica determinada por el número de vértices y lados que se crearán. Inicio. Ejercicios de Geometría - Ejercicios. 17 demostraciones sin palabras del teorema de Pitágoras, con #GeoGebra. Calculadoras Matematicas Online. Les dejo una junta de calculadoras que fui juntando de la web.
Espero q les sirva... Calculadora cientifica (online) Calculadora de vectores (online) También viene con una parte de gráficos y cálculos. Graficador de Vectores (online) Operaciones con Vectores(online) Profile of Miguel Ángel Morales Medina - GeoGebra. Pythagorean theorem water demo. Proyecto Gauss. Demostración ¡hidráulica! del Teorema de Pitágoras. El tan conocido Teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).
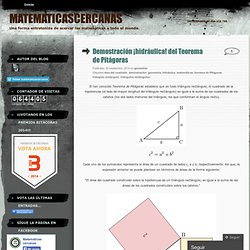
Cada uno de los sumandos representa el área de un cuadrado de lados c, a y b, respectivamente. Así que, la expresión anterior se puede plantear en términos de áreas de la forma siguiente: “El área del cuadrado construido sobre la hipotenusa de un triángulo rectángulo, es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.” Existen muchas demostraciones del Teorema de Pitágoras, a cuál más interesante y sorprendente, partiendo del dibujo anterior. Se trata de demostrar que el área del cuadrado construido sobre la hipotenusa es igual al área que suman los otros dos cuadrados y, por supuesto, hay muchas formas de hacerlo. Así que, como ya he hablado demasiado, os dejo que la veais.
Cómo preparar el desayuno como un matemático. "Euclid: The Game": el juego de las construcciones con regla y compás. Love.jpg (JPEG Image, 510 × 772 pixels) Geometria Euclidiana.