

Integral Calculator: Wolfram Mathematica Online Integrator. Definite Integrals. You might like to read Introduction to Integration first!

Integration Notation After the Integral Symbol we put the function we want to find the integral of (called the Integrand), and then finish with dx to mean the slices go in the x direction (and approach zero in width). Integrals Tutorial. The formal definition of a definite integral is stated in terms of the limit of a Riemann sum.
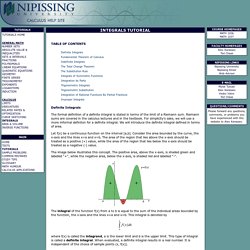
Riemann sums are covered in the calculus lectures and in the textbook. For simplicity's sake, we will use a more informal definiton for a definite integral. Definite Integrals. Calculus I using LiveMath Chapter 5 Since very early history, man has been able to find areas by using classical Greek geometry.

These areas were restricted, however, to shapes that had boundaries of straight line segments and circles. The problem of finding areas under curves, such as those described by continuous functions, could not accurately be solved until calculus was discovered late in the 17th century. There are two methods in calculus that are used to solve these problems. Riemann Sums. Definite Integrals. I once saw a single blade from a turbofan jet engine in the New York City Museum of Modern Art (MOMA).

It was an object of stunning beauty, an engineering and fabrication marvel, and I was compelled to stare at it for a long time. It was smooth and seemingly simple, yet at the same time clearly immensely complicated. The jet engine fan blades on the left (below) and the single windmill blade on the right are three dimensional compound curves, designed for maximum efficiency and the immense strength needed to do their jobs. These complicated. Definite Integrals. Normal Sine Integration. MathScene - Integration - Lesson 3. Lesson 3 Areas between the graphs of functions Areas bounded by the graphs of functions can be found by integration.
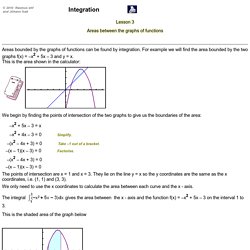
For example we will find the area bounded by the two graphs f(x) = –x2 + 5x – 3 and y = x. This is the area shown in the calculator: We begin by finding the points of intersection of the two graphs to give us the boundaries of the area: –x2 + 5x – 3 = x –x2 + 4x – 3 = 0 Simplify. –(x2 – 4x + 3) = 0 Take –1 out of a bracket. –(x – 1)(x – 3) = 0 Factorise. Summary: The Integral. The Definite Integral as a Sum: Numerical Approach If u is a function of x, we can use the following formula to evaluate an integral.

Riemann Sum If f is a continuous function, the left Riemann sum with n equal subdivisions for f over the interval [a, b] is defined follows. First, partition the interval [a, b] into n equal parts: Δx = (b-a)/n, x0 = a, x1 = a + Δx, x2 = a + 2Δx, ... Next, add up the n products f(x0)Δx, f(x1)Δx, f(x2)Δx, f(xn -1)Δx, to get the Riemann sum. Thus, 4. The Definite Integral. By M.
Integration By Parts Examples, Tricks And A Secret How-To. Integration by parts is a "fancy" technique for solving integrals.
It is usually the last resort when we are trying to solve an integral. The idea it is based on is very simple: applying the product rule to solve integrals. So, we are going to begin by recalling the product rule. Using the fact that integration reverses integration we'll arrive at a formula for integrals, called the integration by parts formula. We'll then solve some examples also learn some tricks related to integration by parts. The Integration by Parts Formula In the following video I explain the idea that takes us to the formula, and then I solve one example that is also shown in the text below. In the video I use a notation that is more common in textbooks. Let's begin by recalling the product rule for derivatives: This formula is easy to memorize. Now, what we have is an equality of two functions.
Let's find the antiderivatives of both sides: Now, arranging this equality: Look at that. Let's see an example. Example 1.