

Paradoxes of set theory. This article contains a discussion of paradoxes of set theory.
As with most mathematical paradoxes, they generally reveal surprising and counter-intuitive mathematical results, rather than actual logical contradictions within modern axiomatic set theory. Basics[edit] Cardinal numbers[edit] Set theory as conceived by Georg Cantor assumes the existence of infinite sets. As this assumption cannot be proved from first principles it has been introduced into axiomatic set theory by the axiom of infinity, which asserts the existence of the set N of natural numbers. (aleph-nought), a number greater than every natural number. Cardinal numbers can be defined as follows. Ordinal numbers[edit] Besides the cardinality, which describes the size of a set, ordered sets also form a subject of set theory. Ordinal numbers can be defined with the same method used for cardinal numbers. Two sets of the same order type have the same cardinality. Power sets[edit] Paradoxes of the infinite set[edit] See also[edit]
Partially ordered set. Zermelo–Fraenkel set theory. In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets free of paradoxes such as Russell's paradox.
Specifically, ZFC does not allow unrestricted comprehension. Today ZFC is the standard form of axiomatic set theory and as such is the most common foundation of mathematics. The consistency of ZFC cannot be proved within ZFC itself. There are many equivalent formulations of the ZFC axioms. Most of the ZFC axioms state the existence of particular sets defined from other sets. The metamathematics of ZFC has been extensively studied. History[edit] In 1908, Ernst Zermelo proposed the first axiomatic set theory, Zermelo set theory. Axioms[edit] All formulations of ZFC imply that at least one set exists. 1. Two sets are equal (are the same set) if they have the same elements.
Fuzzy set. It has been suggested by Thayer Watkins that Zadeh's ethnicity is an example of a fuzzy set because "His father was Turkish-Iranian (Azerbaijani) and his mother was Russian.
His father was a journalist working in Baku, Azerbaijan in the Soviet Union...Lotfi was born in Baku in 1921 and lived there until his family moved to Tehran in 1931. "[5] Definition[edit] A fuzzy set is a pair where is a set and For each the value is called the grade of membership of in For a finite set the fuzzy set is often denoted by Let Then is called not included in the fuzzy set if is called fully included if , and is called a fuzzy member if .[6] The set is called the support of and the set is called its kernel. Injective function. An injective non-surjective function (not a bijection) A function f that is not injective is sometimes called many-to-one.
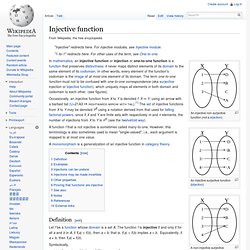
However, this terminology is also sometimes used to mean "single-valued", i.e., each argument is mapped to at most one value. A monomorphism is a generalization of an injective function in category theory. Definition[edit] Symbolically, which is logically equivalent to the contrapositive, Examples[edit] For any set X and any subset S of X the inclusion map S → X (which sends any element s of S to itself) is injective. More generally, when X and Y are both the real line R, then an injective function f : R → R is one whose graph is never intersected by any horizontal line more than once.
Making functions injective. Injections can be undone[edit] Functions with left inverses are always injections. G(f(x)) = x (f can be undone by g) Conversely, every injection f with non-empty domain has a left inverse g (in conventional mathematics[2]). Injections may be made invertible[edit]