

A practical derivation of the Lorentz factor. Penrose–Hawking singularity theorems. The Penrose–Hawking singularity theorems are a set of results in general relativity which attempt to answer the question of when gravitation produces singularities.
A singularity in solutions of the Einstein field equations is one of two things: a situation where matter is forced to be compressed to a point (a space-like singularity)a situation where certain light rays come from a region with infinite curvature (time-like singularity) Space-like singularities are a feature of non-rotating uncharged black-holes, while time-like singularities are those that occur in charged or rotating black hole exact solutions.
Both of them have the following property: geodesic incompleteness: Some light-paths or particle-paths cannot be extended beyond a certain proper-time or affine-parameter (affine parameter is the null analog of proper time). The Penrose theorem guarantees that some sort of geodesic incompleteness occurs inside any black hole, whenever matter satisfies reasonable energy conditions. Cosmic censorship hypothesis. The weak and the strong cosmic censorship hypotheses are two mathematical conjectures about the structure of singularities arising in general relativity.
Singularities that arise in the solutions of Einstein's equations are typically hidden within event horizons, and therefore cannot be seen from the rest of spacetime. Singularities that are not so hidden are called naked. The weak cosmic censorship hypothesis was conceived by Roger Penrose in 1969 and posits that no naked singularities, other than the Big Bang singularity, exist in the universe. Basics[edit] Since the physical behavior of singularities is unknown, if singularities can be observed from the rest of spacetime, causality may break down, and physics may lose its predictive power. The hypothesis was first formulated by Roger Penrose in 1969, and it is not stated in a completely formal way. Weak and strong cosmic censorship hypothesis[edit] Example[edit] The Kerr Metric, corresponding to a black hole of mass and angular momentum .
Deriving the Schwarzschild solution. The Schwarzschild solution is one of the simplest and most useful solutions of the Einstein field equations (see general relativity).
It describes spacetime in the vicinity of a non-rotating massive spherically-symmetric object. It is worthwhile deriving this metric in some detail; the following is a reasonably rigorous derivation that is not always seen in the textbooks. Assumptions and notation[edit] Working in a coordinate chart with coordinates labelled 1 to 4 respectively, we begin with the metric in its most general form (10 independent components, each of which is a smooth function of 4 variables) . (1) A spherically symmetric spacetime is one in which all metric components are unchanged under any rotation-reversal or.
Einstein field equations. The Einstein field equations (EFE) or Einstein - Hilbert equations are a set of 10 equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy.[1] First published by Einstein in 1915[2] as a tensor equation, the EFE equate local spacetime curvature (expressed by the Einstein tensor) with the local energy and momentum within that spacetime (expressed by the stress–energy tensor).[3] As well as obeying local energy-momentum conservation, the EFE reduce to Newton's law of gravitation where the gravitational field is weak and velocities are much less than the speed of light.[4] Exact solutions for the EFE can only be found under simplifying assumptions such as symmetry.
Special classes of exact solutions are most often studied as they model many gravitational phenomena, such as rotating black holes and the expanding universe. Mathematical form[edit] where the scalar curvature, Einstein tensor. Stress–energy tensor. Contravariant components of the stress-energy tensor.
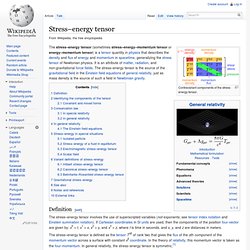
Definition[edit] The stress–energy tensor involves the use of superscripted variables (not exponents; see tensor index notation and Einstein summation notation). If Cartesian coordinates in SI units are used, then the components of the position four-vector are given by: x0 = t, x1 = x, x2 = y, and x3 = z, where t is time in seconds, and x, y, and z are distances in meters. In some alternative theories like Einstein–Cartan theory, the stress–energy tensor may not be perfectly symmetric because of a nonzero spin tensor, which geometrically corresponds to a nonzero torsion tensor.