

A random mathematical blog. Random: Probability, Mathematical Statistics, Stochastic Processes. Welcome!

Random is a website devoted to probability, mathematical statistics, and stochastic processes, and is intended for teachers and students of these subjects. The site consists of an integrated set of components that includes expository text, interactive web apps, data sets, biographical sketches, and an object library. Please read the Introduction for more information about the content, structure, mathematical prerequisites, technologies, and organization of the project. Technologies and Browser Requirements This site uses a number of advanced (but open and standard) technologies, including HTML5, CSS, and JavaScript. F. P. Ramsey, Facts and Propositions. Redundancy theory of truth. According to the redundancy theory of truth (or the disquotational theory of truth), asserting that a statement is true is completely equivalent to asserting the statement itself.
For example, asserting the sentence " 'Snow is white' is true" is equivalent to asserting the sentence "Snow is white". Redundancy theorists infer from this premise that truth is a redundant concept, in other words, that "truth" is a mere word that is conventional to use in certain contexts of discourse but not a word that points to anything in reality. Expected utility hypothesis. In economics, game theory, and decision theory the expected utility hypothesis refers to a hypothesis concerning people's preferences with regard to choices that have uncertain outcomes (gambles).
This hypothesis states that if certain axioms are satisfied, the subjective value associated with a gamble by an individual is the statistical expectation of that individual's valuations of the outcomes of that gamble. This hypothesis has proved useful to explain some popular choices that seem to contradict the expected value criterion (which takes into account only the sizes of the payouts and the probabilities of occurrence), such as occur in the contexts of gambling and insurance.
Daniel Bernoulli initiated this hypothesis in 1738. Until the mid twentieth century, the standard term for the expected utility was the moral expectation, contrasted with "mathematical expectation" for the expected value.[1] Expected value and choice under risk[edit] Bernoulli's formulation[edit] Bayesian Epistemology. 1.

Deductive and Probabilistic Coherence and Deductive and Probabilistic Rules of Inference There are two ways that the laws of deductive logic have been thought to provide rational constraints on belief: (1) Synchronically, the laws of deductive logic can be used to define the notion of deductive consistency and inconsistency. Deductive inconsistency so defined determines one kind of incoherence in belief, which I refer to as deductive incoherence. (2) Diachronically, the laws of deductive logic can constrain admissible changes in belief by providing the deductive rules of inference. For example, modus ponens is a deductive rule of inference that requires that one infer Q from premises P and P → Q. EconPapers: Truth and Probability. Frank P.

Ramsey Chapter 7 in The Foundations of Mathematics and other Logical Essays, 1926, pp 156-198 from McMaster University Archive for the History of Economic Thought Abstract: Contains two other essays as well: Further Considerations & Last Papers: Probability and Partial Belief. Date: 1926References: Add references at CitEc Citations View citations in EconPapers (20) Track citations by RSS feed. Teoría de decisión. Teoría de decisión normativa y descriptiva En contraste, la teoría de decisión positiva o descriptiva se refiere por la descripción de comportamientos observados bajo la asunción que los agentes de toma de decisiones se comportan según algunas reglas consecuentes.
Estas reglas pueden tener, por ejemplo, un marco procesal (p.ej. la eliminación de Amos Tversky por el modelo de aspectos) o un marco axiomático, conciliando los axiomas de Von Neumann-Morgenstern con violaciones behaviorísticas de la hipótesis de utilidad esperada, o pueden dar explícitamente una forma funcional para funciones de utilidad inconsecuentes por el tiempo (p.ej. el descuento cuasi hiperbólico de Laibson). Las nuevas prescripciones o las predicciones sobre el comportamiento que la teoría de decisión positiva produce tienen pruebas adicionales en cuenta de la clase de toma de decisiones que ocurre en la práctica. Qué clases de decisiones necesitan una teoría? Opción bajo incertidumbre Opción intertemporal. Interpretations of Probability (Stanford Encyclopedia of Philosophy/Summer 2003 Edition)
‘Interpreting probability’ is a commonly used but misleading name for a worthy enterprise.

The so-called ‘interpretations of probability’ would be better called ‘analyses of various concepts of probability’, and ‘interpreting probability’ is the task of providing such analyses. Normally, we speak of interpreting a formal system, that is, attaching familiar meanings to the primitive terms in its axioms and theorems, usually with an eye to turning them into true statements about some subject of interest. However, there is no single formal system that is ‘probability’, but rather a host of such systems. To be sure, Kolmogorov's axiomatization, which we will present shortly, has achieved the status of orthodoxy, and it is typically what philosophers have in mind when they think of ‘probability theory’. Belief revision. Belief revision is the process of changing beliefs to take into account a new piece of information.
The logical formalization of belief revision is researched in philosophy, in databases, and in artificial intelligence for the design of rational agents. What makes belief revision non-trivial is that several different ways for performing this operation may be possible. For example, if the current knowledge includes the three facts " is true", " is true" and "if and are true then.
2015 State of the Union Address. I collected tweets about the 2015 State of the Union address [SOTU] in real time from 10am to 2am using the keywords [obama, state of the union, sotu, sotusocial, ernst].
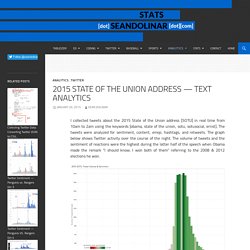
The tweets were analyzed for sentiment, content, emoji, hashtags, and retweets. Odds Probability Calculator. Probability and Statistics — Matter of Stats. Randomness is - as Carl Sagan is oft credited as first declaring - clumpy, and confirmation bias is seductive, so it might be entirely coincidental and partly self-fulfilling that I've lately been noticing common themes in the attitudes towards the statistical models that I create for different people and purposes.
A little context. Some of you will know that as well as building statistical models to predict the outcome of AFL contests as a part-time (sic) hobby, I do similar things during the week, applying those same skills to problems faced by my corporate clients. These clients might, for example, want to identify customers more likely to behave in a specific way - say, to respond to a marketing campaign and open a new product - classify customers as belonging to a particular group or "segment", or talk to customers most at risk of ending their relationship with the client's organisation. For both domains that seems a perfectly reasonable approach to take to prediction. 1. 2. 3. 4. Matter of Stats. "Understanding the Over-round (The Betting Market's Pricing Mechanism)." (2015). Understanding the Overround. In a five horse race, a bookmaker may choose to price up each horse at odds of 4/1 (5.0). In such a scenario, were he to take an equal amount of money on each runner, he would break even, as each horse would have a 20% chance of winning.
In that the five runners have combined implied "probabilities" of winning of 100%, we are dealing with a "round" book. If however, he were to price up each runner at 3/1 (4.0), the implied probabilty of each runner winning will change to 25% from 20%. If he were again to take an equal amount on each runner, he would receive five units and pay out four. The over-round (Vigorish, or simply "vig", or "juice") is what gives the bookmaker his profit, his sun tan and his cigars. Our first example below, focuses on the 2006 Coral Eclipse Stakes, a Group One race run at Sandown Park on July 8 2006. Coral Eclipse Stakes. Determining Bookmaker Implicit Probabilities: The Risk-Equalising Approach — Matter of Stats. In the previous blog I developed a new way of divining a bookmaker's probability assessments of the two teams by assuming that he believes his maximum calibration error - the (negative) difference between his probability assessment for a team and its true probability of victory - is the same for each team in percentage point terms, and that he levies overround on each team's price so as to ensure that it will still deliver an expected profit even if his probability assessment is maximally in error.
This was in contrast to the typical assumption that he levies overround on each team equally. I called this new approach "Risk-Equalising", a tangible example of which might help. Assume that the bookmaker assesses the Home team's probability of victory as being 25% and that he wants an aggregate overround across the two teams to be 5%. Given these numbers he will set the Home team price at about $3.64 and the Away team price at about $1.29. Similarly, for the Away team, we have: Identity #1. Mathematics of bookmaking. In gambling parlance, making a book is the practice of laying bets on the various possible outcomes of a single event. The term originates from the practice of recording such wagers in a hard-bound ledger (the 'book') and gives the English language the term bookmaker for the person laying the bets and thus 'making the book'.[1][2] Making a 'book' (and the notion of overround)[edit] The odds quoted for a particular event may be fixed but are more likely to fluctuate in order to take account of the size of wagers placed by the bettors in the run-up to the actual event (e.g. a horse race).
This article explains the mathematics of making a book in the (simpler) case of the former event. For the second method, see Parimutuel betting It is important to understand the relationship between odds and relative probabilities: Thus, odds of a-b (a/b or a to b) represent a relative probability of b/(a + b), e.g. 6-4 (6 to 4) is 4/(6 + 4) = 4/10 = 0.4 (or 40%). Example[edit] Home: Evens Draw: 2-1. "Understanding the Over-round (The Betting Market's Pricing Mechanism)." (2015).
Odds Converter: Decimal, Fraction, American & Probability. Share This Converter There are 3 methods of stating odds that most bookmakers and websites support. Determining Bookmaker Implicit Probabilities: The Risk-Equalising Approach — Matter of Stats.