

One-way ANOVA in SPSS Statistics - Step-by-step procedure including testing of assumptions. Introduction The one-way analysis of variance (ANOVA) is used to determine whether there are any statistically significant differences between the means of two or more independent (unrelated) groups (although you tend to only see it used when there are a minimum of three, rather than two groups).
For example, you could use a one-way ANOVA to understand whether exam performance differed based on test anxiety levels amongst students, dividing students into three independent groups (e.g., low, medium and high-stressed students). Also, it is important to realize that the one-way ANOVA is an omnibus test statistic and cannot tell you which specific groups were statistically significantly different from each other; it only tells you that at least two groups were different. Since you may have three, four, five or more groups in your study design, determining which of these groups differ from each other is important.
SPSS Statisticstop ^ Assumptions Example Setup in SPSS Statistics. Methods Manual: t-test, hand calculation. Cellular and Molecular Medicine, Department and PhD Graduate Program. Measures of Effect Size (Strength of Association) - Effect Size Calculators. P value calculator. Visual ANOVA. Visual ANOVA Instructions Copyright 1998, 2000 Tom Malloy Note: These instructions are abstracted from and can be supplemented by the full web lecture on the one-way ANOVA for independent groups available through another link on this page.

PRINT: You may print this web page on your local printer if you wish. Visual ANOVA is a simple little program that lets you put all this theory we've been describing into a simple visual whole. It assumes that you've read the Meanings and Intuitions section and have have understood the the general ideas at least.
Right below the "Understanding ANOVA Visually" title are three little buttons labeled MS between, MSwithin, and Instructions. The tool interface is a graph representing a four group study. DRAG THE RED JELLY BEANS. CLICK ON THE YELLOW BUTTONS. The conceptual formula for F is shown below the graph. The current graphic shows a case where the Visual ANOVA tool has been set so that the differences between the means are large. GROUP MEANS. F RATIO. Using ANOVA to Find Differences in Population Means. Chew Jian Chieh February 26, 2010 Three methods used to dissolve a powder in water are compared by the time (in minutes) it takes until the powder is fully dissolved.
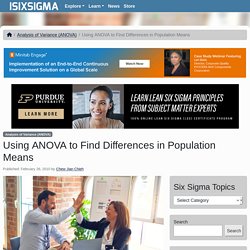
The results are summarized in the following table: It is thought that the population means of the three methods m1, m2 and m3 are not all equal (i.e., at least onem is different from the others). How can this be tested? One way is to use multiple two-sample t-tests and compare Method 1 with Method 2, Method 1 with Method 3 and Method 2 with Method 3 (comparing all the pairs). A better method is ANOVA, which is a statistical technique for determining the existence of differences among several population means. Univariate Statistics - ANOVA Terms. Tell when to use each type of ANOVA, the possible research hypotheses for this statistical model, and when ANOVA can be used to test each type of Research Hypothesis (attributive, associative and causal) Tell when to use each type of ANOVA, the possible research hypotheses for this statistical model, and when ANOVA can be used to test each type of Research Hypothesis (attributive, associative and causal).

A between groups ANOVA should be used when we are comparing one qualitative variable (the IV), and one quantitative variable (the DV), and there are two distinct groups with different participants in each. A within groups ANOVA should be used when each participant is in all of the conditions of the study. The IV and DV remain the same, but in a within groups ANOVA calculation, two DVs will be compared to each other, so two quantitative variables will be assessed. Both types of ANOVA are used to study mean differences between groups.
A BG ANOVA research hypothesis for example will be: females will have higher average means on the Automatic Thoughts Questionnaire than will males. Analysis of Variance Designs. Analysis of Variance Designs Author(s) David M.

Lane Prerequisites. Completely Randomized Anova Design. Completely Randomized Anova Design Ho: m1 = m2 = m3 = = mp vs.

ONE-WAY ANOVA. Analysis of variance (ANOVA) for comparing means of three or more variables.

Use this test for comparing means of 3 or more samples/treatments, to avoid the error inherent in performing multiple t -tests Background. If we have, say, 3 treatments to compare (A, B, C) then we would need 3 separate t -tests (comparing A with B, A with C, and B with C). If we had seven treatments we would need 21 separate t -tests. This would be time-consuming but, more important, it would be inherently flawed because in each t -test we accept a 5% chance of our conclusion being wrong (when we test for p = 0.05). Ideally, for this test we would have the same number of replicates for each treatment , but this is not essential. Analysis of Variance, Monash U. Analysis of Variance (ANOVA) Purpose The reason for doing an ANOVA is to see if there is any difference between groups on some variable. For example, you might have data on student performance in non-assessed tutorial exercises as well as their final grading.
You are interested in seeing if tutorial performance is related to final grade. ANOVA allows you to break up the group according to the grade and then see if performance is different across these grades. Logic of Anova - good. Between Subjects One Way ANOVA example. ANOVA Lecture Notes. ANOVA and Multiple Comparisons Biostatistics BI 45, Saint Anselm College Background Information Analysis of Variance - ANOVA Developed by Fisher while studying agriculture and crop output with different fertilizer treatments, needed test that could evaluate differences between three or more means, developed the F distribution Why - problems with applying the Student's t test to more than 2 sample/population means.

Variance. Variance and the Design of Experiments Contents Variance The F Statistic The Analysis of Variance Power and Sensitivity Designing Experiments - Independent Groups Improving Experimental Designs Using Covariates with Independent Groups Designs Correlated Groups Designs Repeated Measures and Order Effects Complete versus Partial Counterbalancing The Bottom Line Variance When you look at the data from an experiment, the first thing you may notice is that the numbers are not all the same, even for the same condition or the same subject.

There is variability. Variance is a statistic that measures variability. Variance is a measure of variability that can be divided into portions. ANOVA - Statistics Solutions. Meaning of SS (Ho true) 7.4.3.4. 1-Way ANOVA calculations. One-Way ANOVA. How To Calculate and Understand Analysis of Variance (ANOVA) F Test. Between Groups Calculator. Click here to start ANOVA data entryClick here for copy & paste data entry You might guess that the size of maple leaves depends on the location of the trees.

For example, that maple leaves under the shade of tall oaks are smaller than the maple leaves from trees in the prairie and that maple leaves from trees in median strips of parking lots are smaller still. To test this hypothesis you collect several (say 7) groups of 10 maple leaves from different locations. Group A is from under the shade of tall oaks; group B is from the prairie; group C from median strips of parking lots, etc.
Most likely you would find that the groups are broadly similar, for example, the range between the smallest and the largest leaves of group A probably includes a large fraction of the leaves in each group. Where. ANOVA with Excel. Free Analysis of Variance (ANOVA) Calculator - One-Way ANOVA from Summary Data. Anova in Excel - Easy Excel Tutorial. This example teaches you how to perform a single factor ANOVA (analysis of variance) in Excel. A single factor or one-way ANOVA is used to test the null hypothesis that the means of several populations are all equal. Below you can find the salaries of people who have a degree in economics, medicine or history.
H0: μ1 = μ2 = μ3 H1: at least one of the means is different. To perform a single factor ANOVA, execute the following steps. 1. Note: can't find the Data Analysis button? 2. 3. 4. 5. Result: Conclusion: if F > F crit, we reject the null hypothesis.