

Classification des illusions d'optique. Les illusions de couleurs sont très nombreuses et très impressionnantes.

L'illusion de couleur de gauche montre bien ce phénomène. Ce sont les couleurs d'arrière plan qui vont influer sur l'illusion, en effet, la lumière dépend non seulement de l'intensité lumineuse de l'objet lui-même mais aussi de son environnement (contraste de surface). Le cerveau distingue les couleurs par rapport au milieu environnant ainsi le blanc semble accentuer la nuance du carré de gauche et le rouge foncé semble diminuer la nuance du carré de droite. Et c'est la même chose pour l'illusion de dégradé en bas à gauche, le noir éclaircit le gris alors que le blanc semble l'accentuer.
A droite nous voyons des taches grises entre les carrés noirs, ce phénomène découvert il y a plus de 100 ans est désormais un classique. Illusions optique 4eme. Perception du relief et illusions d'optique – C'est pas sorcier. Illusion de Zollner. Un article de Wikipédia, l'encyclopédie libre.
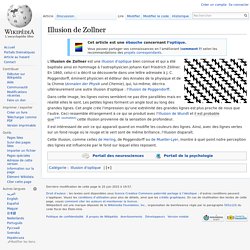
L'illusion de Zollner est une illusion d'optique bien connue et qui a été baptisée ainsi en hommage à l'astrophysicien Johann Karl Friedrich Zöllner. En 1860, celui-ci a décrit sa découverte dans une lettre adressée à J. C. Poggendorff, éminent physicien et éditeur des Annales de la physique et de la Chimie (Annalen der Physik und Chemie), qui, lui-même, décrira ultérieurement une autre illusion d'optique : l'illusion de Poggendorff. Dans cette image, les lignes noires semblent ne pas être parallèles mais en réalité elles le sont. Il est intéressant de voir ce qui apparait quand on modifie les couleurs des lignes. Cette illusion, comme celles de Hering, de Poggendorff ou de Mueller-Lyer, montre à quel point notre perception des lignes est influencée par le fond sur lequel elles reposent. Illusion de Hering. Un article de Wikipédia, l'encyclopédie libre.
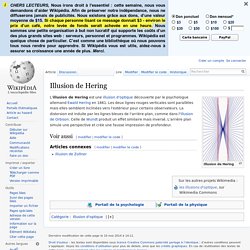
L'illusion de Hering est une illusion d'optique découverte par le psychologue allemand Ewald Hering en 1861. Les deux lignes rouges verticales sont parallèles mais elles semblent inclinées vers l'extérieur pour certains observateurs. Tpeeee. Explications des illusions optico-géométriques. L'impossible escalier - Polygone. Bonjour!
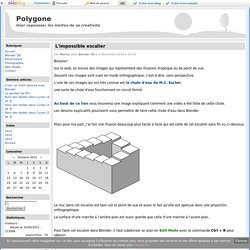
Sur le web, on trouve des images qui représentent des illusions d'optique ou de point de vue. Souvent ces images sont vues en mode orthographique, c'est-à-dire, sans perspective. L'une de ces images qui est très connue est la chute d'eau de M.C. Escher, une sorte de chute d'eau fonctionnant en circuit fermé. Au bout de ce lien vous trouverez une image expliquant comment une vidéo a été faite de cette chute. Les dessins explicatifs pourraient vous permettre de faire cette chute d'eau dans Blender. Mais pour ma part, j'ai fait une illusion beaucoup plus facile à faire qui est celle de cet escalier sans fin vu ci-dessous. Le truc dans cet escalier est bien sûr le point de vue et aussi le fait qu'elle est aperçue dans une projection orthographique. La surface d'une marche à l'arrière-plan est aussi grande que celle d'une marche à l'avant-plan.
Pour faire cet escalier dans Blender, il faut subdiviser un plan en Edit Mode avec la commande Ctrl + R pour obtenir. Triangle de Penrose. Un article de Wikipédia, l'encyclopédie libre.
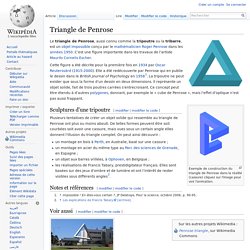
Le triangle de Penrose, aussi connu comme la tripoutre ou la tribarre, est un objet impossible conçu par le mathématicien Roger Penrose dans les années 1950. C’est une figure importante dans les travaux de l’artiste Maurits Cornelis Escher. How To Draw The Impossible Triangle - Optical Illusion. Illusion optique g om triques et artistique, page d'illusion optique 2. Illusions optico-géométriques. ACCUEIL > Différents types d'illusions > Illusions optico-géométriques Illusions optico-géométriques Notre perception visuelle d’un objet peut être altérée par les éléments qui l’entourent.

Ce sont les illusions optico-géométriques. Celles-ci ne naissent pas dans la rétine mais dans le système visuel, lors de la convergence des informations en provenance de chaque œil. Elles ne sont pas liées à notre façon de penser : chaque personne perçoit la même illusion . A- Mise en relation de grandeurs La plupart des illusions optico-géométriques sont fondées sur la mise en relation de grandeurs. 1) Eléments test- éléments inducteurs Dans ces illusions, on compare deux éléments identiques : les éléments test.
Ici, dans l’illusion de Müller-Lyer les deux segments horizontaux qui composent les flèches (éléments test) nous semblent de dimensions différentes. Ils sont pourtant identiques. Illusion optique artistique du triangle impossible de Penrose.