

Quaternion. Heisenberg bohr quantum theory - Pesquisa Google. Copenhagen interpretation. Copenhagen interpretation of quantum mechanics - Recherche Google. Complementarity. Complementarity may refer to: Physical sciences and mathematics[edit] Society and law[edit] Complementarianism, a theological view that men and women have different but complementary rolesComplementary good, a good for which demand is increased when the price of another good is decreasedAn element of interpersonal compatibility in social psychologyThe principle that the International Criminal Court is a court of last resort.
Complementarity bohr. John von neumann wave equation wave function collapse. John von neumann. BKS theory. The Bohr-Kramers-Slater (BKS) theory[1][2][3] was perhaps the final attempt at understanding the interaction of matter and electromagnetic radiation on the basis of the so-called old quantum theory, in which quantum phenomena are treated by imposing quantum restrictions on classically describable behaviour.
It was advanced in 1924, and sticks to a classical wave description of the electromagnetic field. It was perhaps more a research program than a full physical theory, the ideas that are developed not being worked out in a quantitative way. [4]:236 One aspect, the idea of modelling atomic behaviour under incident electromagnetic radiation using "virtual oscillators" at the absorption and emission frequencies, rather than the (different) apparent frequencies of the Bohr orbits, significantly led Born, Heisenberg and Kramers to explore mathematics that strongly inspired the subsequent development of matrix mechanics, the first form of modern quantum mechanics.
Wave function collapse. Process by which a quantum system takes on a definitive state In 1927, Werner Heisenberg used the idea of wave function reduction to explain quantum measurement.[5] However, if collapse were a fundamental physical phenomenon, rather than just the epiphenomenon of some other process, it would mean nature was fundamentally stochastic, i.e. nondeterministic, an undesirable property for a theory.[2][6][7] This issue remained until quantum decoherence entered mainstream opinion after its reformulation in the 1980s.[2][4][8] Decoherence explains the perception of wave function collapse in terms of interacting large- and small-scale quantum systems.[9] Mathematical description[edit] Mathematical background[edit] The quantum state of a physical system is described by a wave function (in turn—an element of a projective Hilbert space).
This can be expressed as a vector using Dirac or bra–ket notation : 1927 paper heisenberg wave function collapse. 1927 paper heisenberg. Uncertainty principle. May 5 1937 einstien. May 5 1937 einstein. Bohr—Kramers—Slater Theory. Bks bohr kramers slater - Recherche Google. Oskar Klein. Oskar Benjamin Klein (Swedish: [klajn]; 15 September 1894 – 5 February 1977) was a Swedish theoretical physicist.[1] Biography[edit] Klein was born in Danderyd outside Stockholm, son of the chief rabbi of Stockholm, Gottlieb Klein from Humenné in Slovakia and Antonie (Toni) Levy.
He became a student of Svante Arrhenius at the Nobel Institute at a young age and was on the way to Jean-Baptiste Perrin in France when World War I broke out and he was drafted into the military. From 1917, he worked a few years with Niels Bohr in the University of Copenhagen and received his doctoral degree at the University College of Stockholm (now Stockholm University) in 1921. In 1923, he received a professorship at University of Michigan in Ann Arbor and moved there with his recently wedded wife, Gerda Koch from Denmark. In 1938, he proposed a boson-exchange model for charge-charging weak interactions (radioactive decay), a few years after a similar proposal by Hideki Yukawa. Five-dimensional space.
Physics[edit] Much of the early work on five dimensional space was in an attempt to develop a theory that unifies the four fundamental interactions in nature: strong and weak nuclear forces, gravity and electromagnetism.
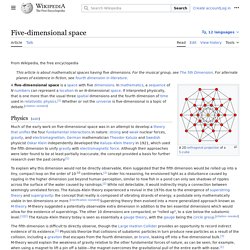
German mathematician Theodor Kaluza and Swedish physicist Oskar Klein independently developed the Kaluza–Klein theory in 1921, which used the fifth dimension to unify gravity with electromagnetic force. Although their approaches were later found to be at least partially inaccurate, the concept provided a basis for further research over the past century.[1] Fifth dimension physics. Eigenvalues and eigenvectors. If the vector space V is finite-dimensional, then the linear transformation T can be represented as a square matrix A, and the vector v by a column vector, rendering the above mapping as a matrix multiplication on the left hand side and a scaling of the column vector on the right hand side in the equation There is a direct correspondence between n-by-n square matrices and linear transformations from an n-dimensional vector space to itself, given any basis of the vector space.
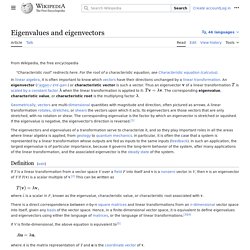
For this reason, it is equivalent to define eigenvalues and eigenvectors using either the language of matrices or the language of linear transformations.[1][2] Geometrically an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction that is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed.[3] Overview[edit] John von Neumann. Eigenstates. Max Abraham. Gustav Mie - Recherche Google. Hilbert space. The state of a vibrating string can be modeled as a point in a Hilbert space.
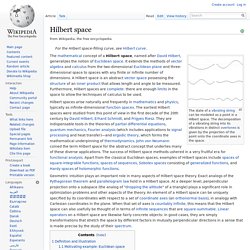
The decomposition of a vibrating string into its vibrations in distinct overtones is given by the projection of the point onto the coordinate axes in the space. Hilbert spaces arise naturally and frequently in mathematics and physics, typically as infinite-dimensional function spaces. The earliest Hilbert spaces were studied from this point of view in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer)—and ergodic theory, which forms the mathematical underpinning of thermodynamics.
John von Neumann coined the term Hilbert space for the abstract concept that underlies many of these diverse applications. Definition and illustration[edit] Hilbert space - Buscar con Google. Jeremy Bernstein. Hendrik Kramers. Schrodinger equation. Eigenvalues. Wave function. Comparison of classical and quantum harmonic oscillator conceptions for a single spinless particle.
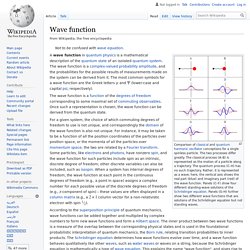
Wave function. Hamiltonian operator. Abraham pais. Schrodinger 1925 quest for the path. Klein gordon equation. Dirac equation. Fermi–Dirac statistics. In quantum statistics, a branch of physics, Fermi–Dirac statistics describes a distribution of particles in certain systems comprising many identical particles that obey the Pauli exclusion principle. It is named after Enrico Fermi and Paul Dirac, who each discovered it independently, although Enrico Fermi defined the statistics earlier than Paul Dirac.[1][2] History[edit] Before the introduction of Fermi–Dirac statistics in 1926, understanding some aspects of electron behavior was difficult due to seemingly contradictory phenomena.
For example, the electronic heat capacity of a metal at room temperature seemed to come from 100 times fewer electrons than were in the electric current.[3] It was also difficult to understand why the emission currents, generated by applying high electric fields to metals at room temperature, were almost independent of temperature. Fermi–Dirac statistics. Pauli exclusion principle. Wolfgang Pauli formulated the law stating that no two electrons can have the same set of quantum numbers.
In the case of electrons in atoms, it can be stated as follows: it is impossible for two electrons of a poly-electron atom to have the same values of the four quantum numbers: n, the principal quantum number, ℓ, the azimuthal quantum number, mℓ, the magnetic quantum number, and ms, the spin quantum number. For example, if two electrons reside in the same orbital, then their n, ℓ, and mℓ values are the same, therefore their ms must be different, and thus the electrons must have opposite half-integer spin projections of 1/2 and −1/2. Particles with an integer spin, or bosons, are not subject to the Pauli exclusion principle: any number of identical bosons can occupy the same quantum state, as with, for instance, photons produced by a laser or atoms in a Bose–Einstein condensate.
Paul Dirac. Enrico Fermi. Fermion spin. Fermion. Antisymmetric wavefunction for a (fermionic) 2-particle state in an infinite square well potential.
In particle physics, a fermion is a particle that follows Fermi–Dirac statistics. These particles obey the Pauli exclusion principle. Fermions include all quarks and leptons, as well as all composite particles made of an odd number of these, such as all baryons and many atoms and nuclei. Fermions differ from bosons, which obey Bose–Einstein statistics. In addition to the spin characteristic, fermions have another specific property: they possess conserved baryon or lepton quantum numbers. As a consequence of the Pauli exclusion principle, only one fermion can occupy a particular quantum state at any given time. Composite fermions, such as protons and neutrons, are the key building blocks of everyday matter. Goudsmit. Uhlenbeck. Spin quanm number - Recherche Google. Borh sommerfeld model of the atom. Borh sommerfeld quanization of rules. Matter Waves – The Physics Hypertextbook. De broglie Combine the two equations for momentum. This was basically Louis de Broglie's doctoral thesis of 1924.
Davisson–Germer experiment. Matter wave. Matter waves are a central part of the theory of quantum mechanics, being an example of wave–particle duality. All matter can exhibit wave-like behavior. Matter waves - Recherche Google. Schrodinger equation for quantum mechanics. Bose seminal paper on photons. Bose seminal.paper on photons - Recherche Google. Lui de droglies matter waves - Google 搜尋.
Bose einstein statistics - Pesquisa Google. Bose einstein statistics - Pesquisa Google. Bose–Einstein statistics. A much simpler way to think of Bose–Einstein distribution function is to consider that n particles are denoted by identical balls and g shells are marked by g-1 line partitions. It is clear that the permutations of these n balls and g − 1 partitions will give different ways of arranging bosons in different energy levels.
Say, for 3 (= n) particles and 3 (= g) shells, therefore (g − 1) = 2, the arrangement might be |●●|●, or ||●●●, or |●|●● , etc. Satyendra Nath Bose - Recherche Google. Ideal gass law - Recherche Google. Quantum statisitical theoey for ideal gasses - Recherche Google. Eintines photoelectric effect - Recherche Google. Spinozas clockwork - Recherche Google. Pascual Jordan. Pascual Jordan matrix mechanics. Observables. Core model. Quantum numbers. The core numbers - Buscar con Google. Orbital frequencies classical and quantum. Werner heisenberg atomic model - Recherche Google. Wolfgang pauli relativity. Wolfgang pauli. Ernest rutherford - Recherche Google. Pieter Zeeman. Bohr sommerfeld model Zeeman effect. Bohr sommerfeld model.
Arnold sommerfeld - Recherche Google. Fritz haber. Pascual Jordan. Max Born. Matrix mechanics. Werner heisenberg. Werner heisenberg matrix mechanics - Recherche Google. Schrodinger electron continuity wave theory. Schrodinger electron continuity. Discontinuity borhs model of the universe. Discontinuity. Pantheism. Spinoza's pantheism.
Democritus atomism - Recherche Google. Democritus. Baruch Spinoza. 17th century philosopher Baruch (de) Spinoza (;[14][15] Dutch: [baːˈrux spɪˈnoːzaː]; Portuguese: [ðɨ ʃpiˈnɔzɐ]; born Baruch Espinosa; later as an author and a correspondent Benedictus de Spinoza, anglicized to Benedict de Spinoza; 24 November 1632 – 21 February 1677[17][18][19][20]) was a Dutch philosopher of Portuguese Sephardi origin.[12] One of the early thinkers of the Enlightenment[21] and modern biblical criticism,[22] including modern conceptions of the self and the universe,[23] he came to be considered one of the great rationalists of 17th-century philosophy.
Inspired by the groundbreaking ideas of René Descartes, Spinoza became a leading philosophical figure of the Dutch Golden Age. Spinoza's given name, which means "Blessed", varies among different languages. In Hebrew, it is written ברוך שפינוזה. Spinoza sephardic. Einstein kant - Pesquisa Google. Einstien spinoza. Ascetic principle definition. Asceticism definition - Recherche Google.