

Antoine Léonard Thomas. René Descartes. Subjectivism. Philosophical position according primacy to human mental activity, rather than shared or communal ones Subjectivism is the doctrine that "our own mental activity is the only unquestionable fact of our experience",[1] instead of shared or communal, and that there is no external or objective truth.
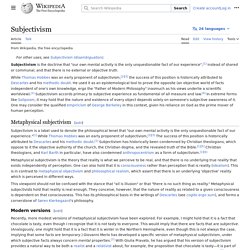
The success of this position is historically attributed to Descartes and his methodic doubt, although he used it as an epistemological tool to prove the opposite (an objective world of facts independent of one's own knowledge, ergo the "Father of Modern Philosophy" inasmuch as his views underlie a scientific worldview).[1] Subjectivism accords primacy to subjective experience as fundamental of all measure and law.[2] In extreme forms like Solipsism, it may hold that the nature and existence of every object depends solely on someone's subjective awareness of it.
[edit] This viewpoint should not be confused with the stance that "all is illusion" or that "there is no such thing as reality. " Fallibilism. Broadly speaking, fallibilism (from Medieval Latin: fallibilis, "liable to err") is the philosophical claim that no belief can have justification which guarantees the truth of the belief.[2] However, not all fallibilists believe that fallibilism extends to all domains of knowledge.
Usage[edit] The term "fallibilism" is used in a variety of senses in contemporary epistemology. The term was coined in the late nineteenth century by the American philosopher Charles Sanders Peirce. Infallibility. Infallibility is the inability to be wrong.
Its importance and meaning is debated in epistemology and major religions. Definition of Infallible by Merriam-Webster. Infallibility. Rus13. THE question as to what we mean by truth and falsehood, which we considered in the preceding chapter, is of much less interest than the question as to how we can know what is true and what is false.

This question will occupy us in the present chapter. There can be no doubt that some of our beliefs are erroneous; thus we are led to inquire what certainty we can ever have that such and such a belief is not erroneous. Sequence. For example, (M, A, R, Y) is a sequence of letters with the letter 'M' first and 'Y' last.
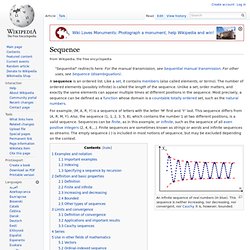
This sequence differs from (A, R, M, Y). Also, the sequence (1, 1, 2, 3, 5, 8), which contains the number 1 at two different positions, is a valid sequence. Sequences can be finite, as in this example, or infinite, such as the sequence of all even positive integers (2, 4, 6,...). Finite sequences are sometimes known as strings or words and infinite sequences as streams. Programming language. The earliest programming languages preceded the invention of the digital computer and were used to direct the behavior of machines such as Jacquard looms and player pianos.[1] Thousands of different programming languages have been created, mainly in the computer field, and many more still are being created every year.
Many programming languages require computation to be specified in an imperative form (i.e., as a sequence of operations to perform), while other languages utilize other forms of program specification such as the declarative form (i.e. the desired result is specified, not how to achieve it). Definitions[edit] A programming language is a notation for writing programs, which are specifications of a computation or algorithm.[2] Some, but not all, authors restrict the term "programming language" to those languages that can express all possible algorithms.[2][3] Traits often considered important for what constitutes a programming language include:
Computer programming. Related tasks include testing, debugging, maintaining a program's source code, implementation of build systems, and management of derived artifacts such as machine code of computer programs.
These might be considered part of the programming process, but often the term software development is used for this larger process with the term programming, implementation, or coding reserved for the actual writing of source code. Software engineering combines engineering techniques with software development practices. History[edit] Programmable devices have existed at least as far back as 1206 AD, when the automata of Al-Jazari were programmable, via pegs and cams, to play various rhythms and drum patterns;[3] and the 1801 Jacquard loom could produce entirely different weaves by changing the "program" - a series of pasteboard cards with holes punched in them.
Data and instructions were once stored on external punched cards, which were kept in order and arranged in program decks. String. From Wikipedia, the free encyclopedia Jump to navigationJump to search String or strings may refer to:
Alphabet. A standard set of letters that represent phonemes of a spoken language Edward Bernard's "Orbis eruditi", comparing all known alphabets as of 1689 The first fully phonemic script, the Proto-Canaanite script, later known as the Phoenician alphabet, is considered to be the first alphabet, and is the ancestor of most modern alphabets, including Arabic, Greek, Latin, Cyrillic, Hebrew, and possibly Brahmic.[1][2] Peter T.
Daniels, however, distinguishes an abugida or alphasyllabary, a set of graphemes that represent consonantal base letters which diacritics modify to represent vowels (as in Devanagari and other South Asian scripts), an abjad, in which letters predominantly or exclusively represent consonants (as in the original Phoenician, Hebrew or Arabic), and an "alphabet", a set of graphemes that represent both vowels and consonants. In this narrow sense of the word the first "true" alphabet was the Greek alphabet,[3][4] which was developed on the basis of the earlier Phoenician alphabet. Sequence. Well-formed formula. Introduction[edit] A key use of formulae is in propositional logic and predicate logics such as first-order logic.
In those contexts, a formula is a string of symbols φ for which it makes sense to ask "is φ true? ", once any free variables in φ have been instantiated. If and only if. Logical connective ↔⇔≡⟺Logical symbols representing iff In logic and related fields such as mathematics and philosophy, if and only if (shortened as iff[1]) is a biconditional logical connective between statements, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence),[2] and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name.
The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. Validity. From Wikipedia, the free encyclopedia Jump to navigationJump to search Validity may refer to: Proof by contradiction. G. H. Hardy described proof by contradiction as "one of a mathematician's finest weapons", saying "It is a far finer gambit than any chess gambit: a chess player may offer the sacrifice of a pawn or even a piece, but a mathematician offers the game.
Trope. Trope or tropes may refer to: Arts and entertainment[edit] Philosophy[edit] Religion[edit] Abstract particulars. Particular. Law of identity. Principia Mathematica. Alfred North Whitehead. English mathematician and philosopher Alfred North Whitehead OM FRS FBA (15 February 1861 – 30 December 1947) was an English mathematician and philosopher. Zeroth-order logic. Set theory. The modern study of set theory was initiated by Georg Cantor and Richard Dedekind in the 1870s. Structure. The structure of a DNA molecule is essential to its function. Load-bearing[edit] A traditional Sami food storage structure. Model theory. This article is about the mathematical discipline.
For the informal notion in other parts of mathematics and science, see Mathematical model. Higher-order logic. The term "higher-order logic", abbreviated as HOL, is commonly used to mean higher-order simple predicate logic. Here "simple" indicates that the underlying type theory is simple, not polymorphic or dependent.[1] Zeroth-order logic. Reference. Pronoun. Noun. Coreference. Referent. Richard Kirkham. Criteria of truth. Principle of bivalence. Human. Non-human. Personal identity. Depersonalization. Self. Wakefulness. Philosophy.
Personhood. Agency. Subjectivity. Qualia. Instantiation principle. Comprehension. Intension. Problem of universals. Property. Quality. Awareness. Consciousness. Ideology. Classical liberalism. Corporation. Collectivism. Totalitarianism. Institution. Society. Sovereignty. Self-governance. Independence. Individualism. Individual. Existentialism. Authenticity. Truth. Propositional attitude. Proposition. Propositional calculus. Theorem. Law of noncontradiction. Contradiction. Constructivism. Constructive proof. Intuitionistic logic. Law of excluded middle. What Are the Three Laws of Logic? Law of thought. Laws of logic.
Laws of thought. Mood. Coherence therapy. Definition of Coherence by Merriam-Webster. Empirical Truth and Revealed Truth. Definition of Empirical Truth by Merriam-Webster. The Nature of Truth and the Different Types of Truth - Fact / Myth. The Nature of Truth. The Nature of Truth: Classic and Contemporary Perspectives. Press.mit. Truth. Memricaprompt. Www.iadvanceseniorcare. 8125f3d0378680e3172fc775d90bcbcf7ee6. Webmd.