

«Optimalité : choix, contraintes, hasard.» un thème où l’on retrouve la déraisonnable efficacité des mathématiques grâce à l’informatique. — Pixees. Trois mots clés qui se fédèrent en une théorie.

©IHP – Maison des mathématiques. Les mathématiques se mettent au service de problèmes concrets pour produire grâce à l’informatique, les meilleures solutions. Choix. Une question ? Contactez-nous ! Jeux à champ moyen : définition wikipédia. Gestion des stocks et de la production intégrant des retours de produits : thèse de Samuel Vercraene, 2012. Mean field games : T. Tao, 2010 [en anglais] John Nash, la théorie des jeux et la question du bon choix : article du Monde, mai 2013. Le mathématicien et prix Nobel John Forbes Nash est mort à l'âge de 86 ans.
L'occasion de revenir sur sa spécialité, la théorie des jeux. LE MONDE SCIENCE ET TECHNO | • Mis à jour le | Philippe Pajot. Cours de Pierre-Louis Lions au Collège de France. Apprentissage automatique et Big Data : Simon Lacoste-Julien, 2014. Algorithmique du style : de nouveaux espaces pour la composition et l’improvisation : François Pachet, 2015.
Les jeux à champ moyen - Brèves de Maths, 2013. Embouteillage en Algarve, Portugal. Dans cette autre brève sur la congestion, il est question d’équilibre atteint par un grand nombre d’automobilistes qui cherchent individuellement à minimiser leur temps de parcours mais qui subissent les conséquences des choix des autres automobilistes via la congestion éventuellement provoquée. En termes physiques, on pourrait voir l’automobiliste dans son véhicule comme une particule qui est soumise à l’action du champ créé par toutes les autres particules (i.e. les autres véhicules). Équilibre de Nash, inventeur du jeu de Hex : Brèves de maths, 2013. John Forbes Nash, Jr.

John Forbes Nash Jr est né en 1928 à Bluefield aux États-Unis, en Virginie-Occidentale. Poussé par ses enseignants sur la voie des mathématiques, il prépare une thèse à l’université de Princeton. Richard Bellman et la programmation dynamique - Brèves de Maths, 2013. Richard Bellman (1920-1984).
Richard Bellman est né le 26 août 1920 à New York. À la fin de ses études universitaires à Baltimore, il est d’abord instructeur des armées avant d’être affecté au projet Manhattan entre 1944 et 1946. Il prépare ensuite une thèse sur les équations différentielles à Princeton sous la direction de Lefschetz et commence une carrière académique. Créer de nouvelles routes peut générer davantage d’embouteillages ou le paradoxe de Braess-Brèves de Maths, 2013. La très fréquentée 42ème rue de New York.
Sa fermeture à la circulation en 1990 a, contre toute attente, fluidifié la circulation. Les embouteillages constituent un véritable fléau pour nos métropoles modernes. Ils ont un coût exorbitant, que ce soit en termes environnementaux ou en temps de travail perdu. Le prix de l'anarchie ou le paradoxe de Braess, Étienne Ghys, 2009. Deux paradoxes Pour expliquer cela, nous allons commencer par décrire un autre phénomène découvert par A.C.

Pigou — un économiste — en 1920 [2]. Dossier thématique sur transport optimal dans Images des mathématiques. Les mathématiques, la clé d'un trafic fluide ? - 31/07/2015 - ladepeche.fr. Si vous prenez la route ce week-end à l'occasion du grand chassé-croisé de l'été et que les centaines de kilomètres de bouchons attendus vous angoissent, rassurez-vous: des mathématiciens tentent d’alléger vos souffrances en définissant des systèmes de régulation du trafic.
Dynamique des fluides, équations aux dérivées partielles, théorie des jeux: autant d'outils mathématiques qui nous dépassent mais pourraient éviter aux automobilistes de rester coincés dans leur voiture...et à l'économie française d'en pâtir. Les embouteillages ont coûté 17 milliards d’euros à l'économie française en 2013, et devraient peser à hauteur de 22 milliards d'ici 2030, selon une étude signée du fournisseur d'information routière INRIX et du Centre for Economics and Business Research (Cebr). Soit plus que le trou de la Sécu en 2014. "J'étudie des équations qui décrivent l'écoulement d'un gaz ou d'un fluide", explique-t-elle à l'AFP. 'comportement égoïste'
Création d'un Inria Innovation Lab pour réduire la consommation en carburant des avions. Partenariat Recherche - Industrie Le partenariat entre Safety Line et l’équipe de recherche COMMANDS se concrétise aujourd’hui par la création d’un Inria Innovation Lab.
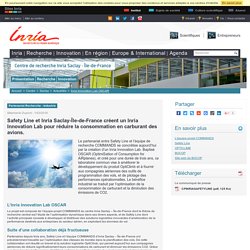
Baptisé OSCAR (OptimiSation of Consumption for AiRplanes), et créé pour une durée de trois ans, ce laboratoire commun vise à améliorer le développement du produit OptiClimb et à fournir aux compagnies aériennes des outils de programmation des vols, et de pilotage des performances opérationnelles. Le bénéfice industriel se traduit par l’optimisation de la consommation de carburant et la diminution des émissions de CO2. Convexité et optimisation : cours de Guy Cohen, 2000, corr. 2006. Optimisation et apprentissage : Alexandre d'Aspremont, 2014. La programmation par contraintes expliquée à ma garagiste ou à mon fleuriste : Charlotte Truchet, 2015.
Parmi les grandes familles d'approches et de langages informatiques, on entend parfois parler de « programmation par contraintes ».
Un chercheur du domaine vous expliquerait peut-être que « c'est un paradigme de programmation déclarative permettant de traiter des problèmes fortement combinatoires ». Euh... Heureusement, Binaire a son joker : une enseignante-chercheure Charlotte Truchet, spécialiste du domaine, qui sait expliquer ses recherches. La programmation par contraintes : Étienne Parizot, Sylvain Soliman, François Fages, 2004. Lorsque les contraintes sont nombreuses, la résolution d'un problème est en pratique très difficile.
Surtout si on exige de trouver la meilleure solution possible... © potowizard - Fotolia.com. Optimisation : quand le mieux n'est pas l'ennemi du bien : conférence Pierre Martinon, 2009. Conception interactive d’environnements urbains durables à base de résolution de contraintes : thèse de Bruno Belin, 2014. Publications dans les conférences JFPC (Journées Francophones de Programmation par Contraintes) Colisweb améliore son modèle de livraison avec Inria. Collaboration © Colisweb C’est un problème complexe que Colisweb a soumis à l’équipe Inocs d’Inria Lille - Nord Europe : déterminer à l’avance le planning d’une flotte de livreurs, sans connaître leur charge de travail.
Objectif : proposer des livraisons immédiates sans surcoût. Algorithme génétique : définition wikipédia. Origines[modifier | modifier le code] La popularisation des algorithmes génétiques sera l'œuvre de David Goldberg à travers son livre Genetic Algorithms in Search, Optimization, and Machine Learning[1] (1989). Ce livre est encore édité aujourd'hui. En Europe, la première conférence sur ce type de sujet fut l'European Conference on Artificial Life en 1991 (elle a fêté ses 20 ans en 2011[2]), coorganisée par Francisco Varela et Paul Bourgine. Le hasard fait bien les choses : exposé de Corinne Touati (vidéo 1), 2013.
Le hasard fait bien les choses : 1ère partie Cet exposé porte sur la "théorie des jeux" ou, plus simplement, "comment modéliser un système mettant en jeu des acteurs en interaction? ". Nous montrons tout d'abord quelques exemples introductifs à la théorie des jeux et les éventuelles conséquences néfastes de la multiplication des preneurs de décisions en terme d'efficacité globale. Dans une seconde partie, nous présentons succinctement quelques applications de ces phénomènes dans des problèmes de ressources dans les réseaux de télécommunication et montrons notamment au travers du problème d'association entre mobiles (téléphone, ordinateur...) et stations de base (antenne du fournisseur d'accès) dans les réseaux sans-fils comment l'ajout de hasard dans la prise de décision permet d'aboutir à des allocations optimales. Le hasard fait bien les choses : exposé de Corinne Touati (vidéo 2), 2013.
Le hasard fait bien les choses : 2ème partie Cet exposé porte sur la "théorie des jeux" ou, plus simplement, "comment modéliser un système mettant en jeu des acteurs en interaction? ". Nous montrons tout d'abord quelques exemples introductifs à la théorie des jeux et les éventuelles conséquences néfastes de la multiplication des preneurs de décisions en terme d'efficacité globale. Dans une seconde partie, nous présentons succinctement quelques applications de ces phénomènes dans des problèmes de ressources dans les réseaux de télécommunication et montrons notamment au travers du problème d'association entre mobiles (téléphone, ordinateur...) et stations de base (antenne du fournisseur d'accès) dans les réseaux sans-fils comment l'ajout de hasard dans la prise de décision permet d'aboutir à des allocations optimales.
Le hasard fait bien les choses : Denis Talay, 2009. La conquête du hasard : Fernando Corbalán, Gerardo Sanz, 2013. Introduction à la théorie des jeux : Sébastien Konieczny. Les mathématiques de l'évolution : documentaire de Régis Ferrière. Hasard et chance du 27 juin 2016 - France Inter. Peut-on calculer le hasard ? France culture 8/12/2016. Références bibliographiques.