

Jim Plank's Origami Page (Modular) How To Make Intersecting Planes Models. Sonobe module. Instuctions for making this model Below is the Sonobe unit, designed by Mitsonobu Sonobe, which I learned from Kazuyo Inoue.

Above is the capped icosahedron which she made for me from this unit; you need to make about 30 units for this, but you only need six if you want to make a cube. Since this must be very well known, I'm only putting a very brief picture of how to make it. Platonic Solid. The Platonic solids, also called the regular solids or regular polyhedra, are convex polyhedra with equivalent faces composed of congruent convex regular polygons.
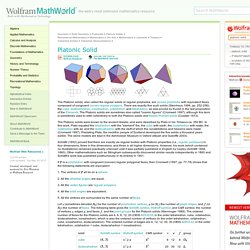
There are exactly five such solids (Steinhaus 1999, pp. 252-256): the cube, dodecahedron, icosahedron, octahedron, and tetrahedron, as was proved by Euclid in the last proposition of the Elements. The Platonic solids are sometimes also called "cosmic figures" (Cromwell 1997), although this term is sometimes used to refer collectively to both the Platonic solids and Kepler-Poinsot solids (Coxeter 1973). Jim Plank's Origami Page (Modular) Math Craft Monday: Community Submissions (Plus How to Make a Modular Origami Intersecting Triangles Sculpture) Math Craft Monday: Community Submissions (Plus How to Make a Modular Origami Intersecting Triangles Sculpture) It's once again Monday, which means it's time to highlight some of the most recent community submissions posted to the Math Craft corkboard.
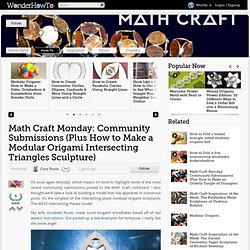
I also thought we'd take a look at building a model that has appeared in numerous posts. It's the simplest of the intersecting plane modular origami sculptures: The WXYZ Intersecting Planes model. My wife, Elizabeth Poole, made some kirigami snowflakes based off of last week's instructions. She posted up a few examples for everyone. I made a few more, as well.
My wife also gave me an idea—making snowflakes based off of tessellations. Justin Meyers of Scrabble World posted up a link to a really cool how-to on making beautiful origami Christmas trees. Here's a "quick" version I made. Rachel Mansur posted up a plethora of links to some amazing origami artworks. Or maybe it was this picture of a giant Sonobe icosahedron: Materials and Tools. Www.papierfalten.de/documents/faltanleitungen/margarete_stern.pdf. Www.origami.gr.jp/Archives/Etc/convention02/SR_Dodecahedron1.pdf. Dev.origami.com/images_pdf/tematebaku. Www.origamee.net/diagrams/cubes/meecube2.html. Thatch Cube.

UVWXYZ diagrams2. UVWXYZ diagrams1. Www.origamee.net/diagrams/cubes/meecube4.html. Whirl Cube.
Wolbashi - unit by *wolbashi on deviantART. XYZmbe by Nick Robinson. Folding Modular Models - Polyhedrals by Francis Ow. Folding Modular Models - Polyhedrals This page has many graphics and illustrate how to fold a few simple models.

Due to its graphical nature, loading of this page will be slow. Modular models are where simple modules are first folded, these simple modules are then lock together without the use of glue to form the complete model. I have created many modular creations using different number of simple modules. I have also created many Polyhedral Models using modules. Polyhedral Models Folding are a subset of Modular Models Folding. Diagrams avaliable here include: 120 degrees module - to construct truncated tetrahedron, cuboctahedron, dodecahedron, rhombicuboctahedron, etc. How to fold a 120-degree module Using this module and folding the required number modules you can construct a Truncated Tetrahedron, Cuboctahedron, Dodecahedron, Rhombicuboctahedron, etc. How to fold a 135-degree module I wish you luck and many hours of happy frustrating fun! Isosceles Triangle Unit. Copyright © 2002 by M.

Mukhopadhyay. All rights reserved. Here are some YouTube instructions by Karl. 30 Unit Assemblies: Greater Stellated Dodecahedron with 45 degree unit, Lesser Stellated Dodecahedron with 36 degree unit, Rhombic Triacontahedron with rhombic unit. Isos.gif (526×701) Www.origamee.net/diagrams/cootie.html. Cootie Catcher Ball Make 12 or 30 units of the traditional Cootie Catcher or Fortune Teller.

Assemble them to get these finished models. Remember that when you assemble diagonally opposite "wings" are either both over or both under. You can find instructions for folding Fortune Tellers in many sites including Enchanted Learning, if you do not already know how to fold one. Good luck! Two Thirds Sonobe. Copyright © 2001 by M.

Mukhopadhyay. All rights reserved. Definitions of mountain fold, valley fold and preliminary bases can be found in Origami For Everyone. Www.origamee.net/diagrams/sonobes/sonobe3.html. Sonobe Variation Copyright (c) 1999 by M.
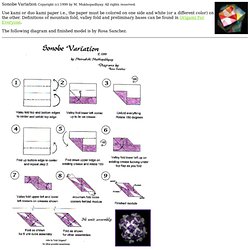
Mukhopadhyay.