

Zome Uniform Polyhedra. Www.software3d.com/JPeg/RotDrill. Spherical polyhedron. This beach ball shows a hosohedron with six lune faces, if the white circles on the ends are removed.
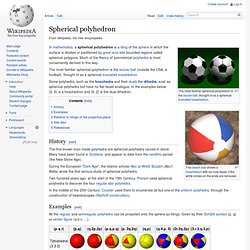
In mathematics, a spherical polyhedron is a tiling of the sphere in which the surface is divided or partitioned by great arcs into bounded regions called spherical polygons. Much of the theory of symmetrical polyhedra is most conveniently derived in this way. The most familiar spherical polyhedron is the soccer ball (outside the USA, a football), thought of as a spherical truncated icosahedron. Some polyhedra, such as the hosohedra and their duals the dihedra, exist as spherical polyhedra but have no flat-faced analogue. In the examples below, {2, 6} is a hosohedron and {6, 2} is the dual dihedron. History[edit] The first known man-made polyhedra are spherical polyhedra carved in stone. During the European "Dark Age", the Islamic scholar Abū al-Wafā' Būzjānī (Abu'l Wafa) wrote the first serious study of spherical polyhedra.
Examples[edit] Relation to tilings of the projective plane[edit] L. N-sphere. In mathematics, the n-sphere is the generalization of the ordinary sphere to a n-dimensional space.
For any natural number n, an n-sphere of radius r is defined as the set of points in (n + 1)-dimensional Euclidean space which are at distance r from a central point, where the radius r may be any positive real number. Thus, the n-sphere centred at the origin is defined by: It is an n-dimensional manifold in Euclidean (n + 1)-space. In particular: Spherical coordinate system.
Spherical coordinates (r, θ, φ) as commonly used in physics: radial distance r, polar angle θ (theta), and azimuthal angle φ (phi).
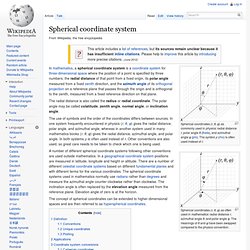
The symbol ρ (rho) is often used instead of r. Spherical coordinates (r, θ, φ) as often used in mathematics: radial distance r, azimuthal angle θ, and polar angle φ. The meanings of θ and φ have been swapped compared to the physics convention. In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its polar angle measured from a fixed zenith direction, and the azimuth angle of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the zenith, measured from a fixed reference direction on that plane.
Plot trajectories on a sphere? Math Forum Discussions - Matlab sphere plot. Math Forum Discussions - Re: How to plot points on a sphere? Waterman polyhedron. Waterman polyhedra are created by packing spheres according to the cubic close(st) packing (CCP), then sweeping away the spheres that are farther from the center than a defined radius.[1] The resulting pack of spheres is then convex hulled, and thereby a polyhedron is created.
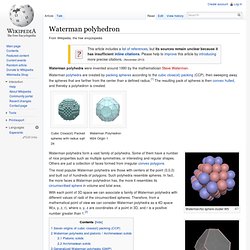
Cubic Close(st) Packed spheres with radius sqrt 24Waterman Polyhedron W24 Origin 1 Waterman/fcc sphere cluster W5 Waterman/fcc polyhedra interpretation of sphere cluster w5 Waterman polyhedra form a vast family of polyhedra. Some of them have a number of nice properties such as multiple symmetries, or interesting and regular shapes. The most popular Waterman polyhedra are those with centers at the point (0,0,0) and built out of hundreds of polygons.
With each point of 3D space we can associate a family of Waterman polyhedra with different values of radii of the circumscribed spheres. Seven origins of cubic close(st) packing (CCP)[edit] There can be seven origins defined in CCP,[3] where n = {1, 2, 3, …}: Notes[edit] Sam's Personal Page. This was more my dad's hobby than mine, really, but it's an interesting topic and a fun way to spend a weekend or two.

Both of us had an interest in building domes for quite a time; I remember my dad working on the plans for a dome probably before my teenage years. Before he died he made a selection of geodesic domes, and developed a cheap, quick and simple method for constructing the frame of a fairly tough geodesic dome. Hoberman sphere. Hoberman sphere, working plastic model A Hoberman sphere is an isokinetic structure patented by Chuck Hoberman that resembles a geodesic dome, but is capable of folding down to a fraction of its normal size by the scissor-like action of its joints.
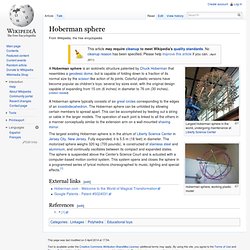
Colorful plastic versions have become popular as children's toys: several toy sizes exist, with the original design capable of expanding from 15 cm (6 inches) in diameter to 76 cm (30 inches). [citation needed] Sphere. A sphere is defined as the set of all points in three-dimensional Euclidean space that are located at a distance (the "radius") from a given point (the "center").
Twice the radius is called the diameter, and pairs of points on the sphere on opposite sides of a diameter are called antipodes. Unfortunately, geometers and topologists adopt incompatible conventions for the meaning of "