

Et si demain on roulait sur des routes... en plastique? Va-t-on bientôt rouler sur des routes en plastique ?
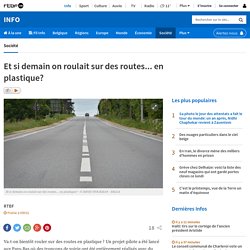
Un projet-pilote a été lancé aux Pays-Bas où des tronçons de voirie ont été entièrement réalisés avec du plastique recyclé (voir la vidéo ci-dessous). La Région wallonne s'intéresse de près à cette expérience qui pourrait être révolutionnaire. Rapidité de construction, facilité de réparation... l'idée comporte de nombreux avantages. Newsletter info Recevez chaque jour toutes les infos du moment Recevoir "Les routes en plastique sont préfabriquées, un peu comme des Lego, comme les jeux d’enfants qui s’emboîtent, donc l’installation est à peu près 5 à 6 fois plus rapide que la construction d’une route normale", explique Pasquale Nardonne, physicien à l’ULB.
Autre atout : la facilité de réparation d'un tronçon endommagé. Autre argument phare : l'aspect écologique de cette innovation. "Ça coûte cher" Reste cette question : est-ce que le plastique va résister à la pression des poids lourds ? Bzscrse. Bzscrse. Distributions statistiques des particules/Statistique de Fermi-Dirac — Wikiversité. Une page de Wikiversité.
Début de la boite de navigation du chapitre fin de la boite de navigation du chapitre En raison de limitations techniques, la typographie souhaitable du titre, « Distributions statistiques des particules : Statistique de Fermi-DiracDistributions statistiques des particules/Statistique de Fermi-Dirac », n'a pu être restituée correctement ci-dessus. La statistique de Fermi-Dirac décrit le comportement de ce qu'on appelle les fermions. les fermions sont des particules de spin demi-entier tel que les électrons. Ces particules possèdent des caractéristiques particulières. Ils ne peuvent pas occuper le même espace quantique. En effet, selon les lois thermodynamiques tout système tend à obtenir le niveau d'énergie le plus bas possible (par exemple : un objet tombe jusqu'à arriver le plus bas qu’il puisse). La démonstration ci-après est basée sur celle de Rocard[1] Dénombrement des états[modifier | modifier le wikicode] Soit une boîte contenant une seule case.
Où en posant. Cours n°1 : La naissance de la physique quantique. Cours n°2 : Le formalisme de la physique quantique. Cours n°3 : L'interprétation de la physique quantique. Phy1352 ed formulaire. Rotationnel. Research Quantum Experience. Récolte.
Berkeley Physique Statistique F Reif. Principles of Quantum Mechanics Dirac. Mécanique quantique - Basdevant et Daliband - Ecole Polytechnique. MonCoursMQ. Aide mémoire. Loi de distribution des vitesses de Maxwell. Théorie cinétique des gaz. Densité de probabilité canonique. Mécanique hamiltonienne. Un article de Wikipédia, l'encyclopédie libre.
Pour les articles homonymes, voir Hamilton. La mécanique hamiltonienne, inventée par William Rowan Hamilton en 1833, est une reformulation de la mécanique classique. Son formalisme a facilité l'élaboration théorique de la mécanique quantique. Équations canoniques de Hamilton[modifier | modifier le code] Rappels de mécanique lagrangienne[modifier | modifier le code] et des vitesses correspondantes , où Le lagrangien peut donc s'écrire formellement comme une fonction : , les variables indexées représentant les variables de ce type.
Moment conjugué[modifier | modifier le code] En mécanique hamiltonienne, chaque vitesse généralisée est remplacée par la quantité de mouvement associée, aussi appelée moment conjugué ou encore impulsion généralisée : Hamiltonien[modifier | modifier le code] L'hamiltonien est la transformée de Legendre du lagrangien : Si les équations qui définissent les coordonnées généralisées sont indépendantes du temps t, on peut montrer que à. Lagrangien. Un article de Wikipédia, l'encyclopédie libre.
Le lagrangien Les équations du mouvement[modifier | modifier le code] Considérons un système dynamique repéré par des paramètres de position . Au cours du temps, ces paramètres varient, leur taux de variation étant . Du système est constitué des , des. Équations de Maxwell. Un article de Wikipédia, l'encyclopédie libre.
Les équations de Maxwell, aussi appelées équations de Maxwell-Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l'électromagnétisme, avec l'expression de la force électromagnétique de Lorentz. Ces équations montrent notamment qu'en régime stationnaire, les champs électrique et magnétique sont indépendants l'un de l'autre, alors qu'ils ne le sont pas en régime variable.
Dans le cas le plus général, il faut donc parler du champ électromagnétique, la dichotomie électrique/magnétique étant une vue de l'esprit. Cet aspect trouve sa formulation définitive dans le formalisme covariant présenté dans la seconde partie de cet article : le champ électromagnétique y est représenté par un être mathématique unique : le tenseur électromagnétique, dont certaines composantes s'identifient à celles du champ électrique et d'autres à celles du champ magnétique. Phy1352 ed formulaire.
Richard P Feynman: Quantum Mechanical View of Reality 1 (Part 1)