

GUI per MATLAB. PID Control of Physics Bodies - gamedev.net. Does anyone use a PID-Controller in games? : gamedev. Simon's Tech Blog: Using PID Controller. Introduction Several weeks ago, I need to implement a game screen for user to choose a level.
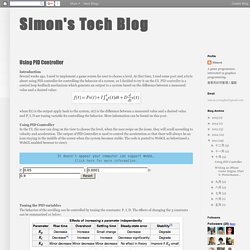
At that time, I read some post and article about using PID controller for controlling the behavior of a system, so I decided to try it on the UI. PID controller is a control loop feedback mechanism which generate an output to a system based on the difference between a measured value and a desired value: where f(t) is the output apply back to the system, e(t) is the difference between a measured value and a desired value and P, I, D are tuning variable for controlling the behavior. More information can be found on this post. Using PID Controller In the UI, the user can drag on the view to choose the level, when the user swipe on the icons, they will scroll according to velocity and acceleration. Tuning the PID variables The behavior of the scrolling can be controlled by tuning the constants: P, I, D.
Reference: [1]: [2]: [3]: [4]: Game Math: Numeric Springing Examples. This post is part of my Game Math Series.
So, you have seen how to precisely control numeric springing in my previous post. I showed this animation as an example. Manually fine-tuning the animation with animation curves can possibly give better results, if it’s a fixed animation, that is. One big advantage of numeric springing over animation curves is that it can be dynamic and interactive. For instance, when the springing simulation has not completely come to a stop, and you poke the system (modify the target value or velocity) based on user input, the system can handle it gracefully with numeric springing and everything looks natural.
I will show you several examples of numeric springing in this post. Before that, let’s quickly review the spring function presented in my previous post. Positional Springing We can dynamically set the target position based on user input and have object spring to the target position accordingly. PID Math Demystified. Controlling Self Driving Cars. Simple Examples of PID Control. Controlli automatici - WikiAppunti. [controlli] Di R. de Simone. Simulation of PID Control Applied to Irrigation Channels. Volume 70, 2014, Pages 978–987 12th International Conference on Computing and Control for the Water Industry, CCWI2013 Edited By Bruno Brunone, Orazio Giustolisi, Marco Ferrante, Daniele Laucelli, Silvia Meniconi, Luigi Berardi and Alberto Campisano Abstract Open-channel flow usually includes many hydraulic elements to help with the regulation of water supply in terms of automatic control.

On the other hand, the one-dimensional Shallow Water Equations (SWE) are widely used to model and predict the flow dynamics in this kind of configurations. Keywords PID; Irrigation Channels; Calibration; Simulation; Shallow Water Equations References. Controllo PID. Da Wikipedia, l'enciclopedia libera.
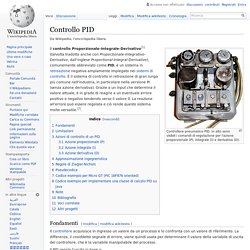
Controllore pneumatico PID. In alto sono visibili i comandi di regolazione per l'azione proporzionale (P), integrale (I) e derivativa (D). Il controllo Proporzionale-Integrale-Derivativo[1] (talvolta tradotto anche con Proporzionale-Integrativo-Derivativo, dall'inglese Proportional-Integral-Derivative), comunemente abbreviato come PID, è un sistema in retroazione negativa ampiamente impiegato nei sistemi di controllo.
È il sistema di controllo in retroazione di gran lunga più comune nell'industria, in particolare nella versione PI (senza azione derivativa). Grazie a un input che determina il valore attuale, è in grado di reagire a un eventuale errore positivo o negativo tendendo verso il valore 0. Fondamenti[modifica | modifica wikitesto] Il PID regola l'uscita in base a: Controllo robusto. Microcontrollore. Da Wikipedia, l'enciclopedia libera.
In elettronica digitale il microcontrollore o microcontroller o MCU (MicroController Unit) è un dispositivo elettronico integrato su singolo chip, nato come evoluzione alternativa al Microprocessore ed utilizzato generalmente in sistemi embedded ovvero per applicazioni specifiche (special purpose) di controllo digitale. Descrizione[modifica | modifica wikitesto] Generalmente sono dotati di CPU CISC con architettura von Neumann, anche se più di recente sono apparsi microcontrollori con CPU ad architettura RISC, come ad esempio il Texas Instruments MSP430, meglio predisposti per l'utilizzo dei moderni compilatori, piuttosto che dell'Assembly.
Taluni microcontrollori complessi (come il Freescale 68302) hanno un processore RISC separato dal processor core. Per i microcontrollori sono pubblicati sistemi di sviluppo amatoriali e professionali anche in modalità open source. Cenni storici[modifica | modifica wikitesto] Il primo microcontrollore. Funzione di trasferimento. Linear Algebra and Least Squares - MATLAB & Simulink - MathWorks Italia.