

The Reference Frame: Proof of RH from Hurwitz eigenstates. Under my previous (QM-on-graphs) blog post about the Riemann Hypothesis, Dilaton was forgiven for having brought us some cute internet banalities ;-) while Akhmeteli pointed out a paper that seems even more promising than my most recent specific attacks: Hamiltonian for the zeros of the Riemann zeta function In their PRL paper, Carl M.
Bender, Dorje C. Brody, and Markus P. Wa report01 08. Timescalewiki.
The Home of Mathematical Knitting. The Home of Mathematical Knitting (sarah-marie's mathematical knitting pages and mathematical fiber arts pages) Conference Sessions and Books Carolyn Yackel and sarah-marie belcastro co-organized three mathematics conference sessions, each of which included a sequence of talks and a mathematical fiber arts exhibit.

We have co-edited two books on mathematics and fiber arts written for crafters, mathematicians, and mathematics educators. Scale. Power laws and the generalized CLT. Here’s an expert from a recent ACM Ubiquity interview with David Alderson that raises a few questions.

Actually, they [power laws] aren’t special at all. They can arise as natural consequences of aggregation of high variance data. You know from statistics that the Central Limit Theorem says distributions of data with limited variability tend to follow the Normal (bell-shaped, or Gaussian) curve. There is a less well-known version of the theorem that shows aggregation of high (or infinite) variance data leads to power laws. Thus, the bell curve is normal for low-variance data and the power law curve is normal for high-variance data.
In this post I will explain the theory I believe Alderson is alluding to in his informal remarks. I don’t understand what Alderson has in mind when he refers to data with high but finite variance. The Generalized CLT says that if the “aggregation” converges to a non-degenerate distribution, that distribution must be a stable distribution. Nombre presque entier. Un article de Wikipédia, l'encyclopédie libre.
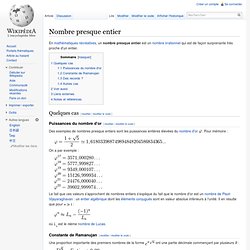
En mathématiques récréatives, un nombre presque entier est un nombre irrationnel qui est de façon surprenante très proche d'un entier. Quelques cas[modifier | modifier le code] Puissances du nombre d'or[modifier | modifier le code] Des exemples de nombres presque entiers sont les puissances entières élevées du nombre d'or . Anal0405.
Moyenne logarithmique. Bayes' theorem. Assessment | Biopsychology | Comparative | Cognitive | Developmental | Language | Individual differences | Personality | Philosophy | Social |Methods | Statistics | Clinical | Educational | Industrial | Professional items | World psychology | Statistics:Scientific method · Research methods · Experimental design · Undergraduate statistics courses · Statistical tests · Game theory · Decision theory Bayes' theorem (also known as Bayes' rule or Bayes' law) is a result in probability theory, which relates the conditional and marginal probability distributions of random variables.
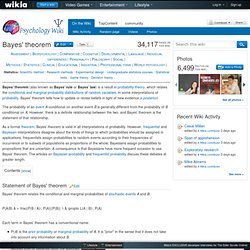
In some interpretations of probability, Bayes' theorem tells how to update or revise beliefs in light of new evidence a posteriori. As a formal theorem, Bayes' theorem is valid in all interpretations of probability. Phyllotaxis system01. From Wikipedia "In botany, phyllotaxis or phyllotaxy is the arrangement of the leaves on the stem of a plant.

I'm working on phyllotaxis system in order to construct vertical spiral variations with a rhinoscript code: -plot an array of points by x,y,z coordinates follwing mathematical logic with several variations. The Funnel Surface. Tour à pression constante. SURFACE DE LA TOUR À PRESSION CONSTANTE, ou ENTONNOIRConstant pressure tower surface or funnel surface, Fläche des Turms mit konstantem Druck oder Trichterfläche La tour à pression constante est la surface de révolution obtenue en faisant tourner une logarithmique autour de son asymptote.Son nom vient de ce que, cette surface étant remplie d'un matériau homogène, la pression exercée sur toute section horizontale par la partie supérieure est constante.
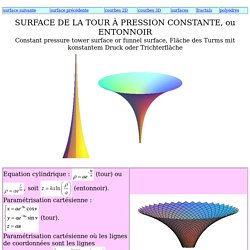
Voir aussi la trompette de Gabriel. © Robert FERRÉOL 2012. HOME. Set Theory and Foundations of Mathematics. Angle solide. Un article de Wikipédia, l'encyclopédie libre.
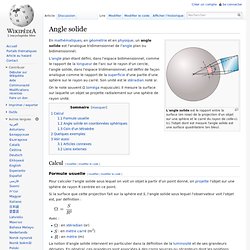
L'angle solide est le rapport entre la surface (en rose) de la projection d'un objet sur une sphère et le carré du rayon de celle-ci. Ici, l'objet dont est mesuré l'angle solide est une surface quadrilatère (en bleu). En mathématiques, en géométrie et en physique, un angle solide est l'analogue tridimensionnel de l'angle plan ou bidimensionnel. L'angle plan étant défini, dans l'espace bidimensionnel, comme le rapport de la longueur de l'arc sur le rayon d'un cercle, l'angle solide, dans l'espace tridimensionnel, est défini de façon analogue comme le rapport de la superficie d'une partie d'une sphère sur le rayon au carré.
Son unité est le stéradian noté sr. On le note souvent Ω (oméga majuscule). Identité d'Euler: approche. Identité d'Euler. Un article de Wikipédia, l'encyclopédie libre.
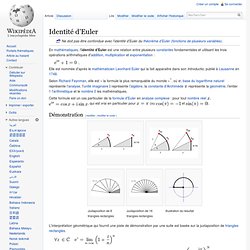
En mathématiques, l'identité d'Euler est une relation entre plusieurs constantes fondamentales et utilisant les trois opérations arithmétiques d'addition, multiplication et exponentiation : Elle est nommée d'après le mathématicien Leonhard Euler qui la fait apparaitre dans son Introductio, publié à Lausanne en 1748. Cette formule est un cas particulier de la formule d'Euler en analyse complexe : pour tout nombre réel , qui est vrai en particulier pour (ou. Site mathématique de la classe MPSI du lycée Paul Valéry de Paris.
Indicateur d'Euler-Poincaré. Nous venons de voir qu'une courbe ouverte se contracte en un point.

Et la courbe fermée? On se souvient de la règle: elle doit se contracter sur elle-même, sur sa propre trace. Il est possible de la faire tourner sur son sillage, mais … Impossible de la rétrécir à un seul point. La taille de la boucle peut être réduite autant que l'on veut. Alors, que faire de la courbe fermée? Mais alors nous devons matérialiser le coup de ciseaux par un point et, il restera une courbe ouverte, deux éléments de base de la topologie. Note: La courbe ouverte obtenue est un élément de base de dimension 1; elle est témoin de cette dimension.
Une courbe ouverte peut se contracter en un point. Mais, peut-on la décomposer? La courbe fermée se décompose en deux éléments de base: Un point – dimension 0, et Un segment – dimension 1.
Exponential function. Et si on rajoutait une droite à l'infini ? Pourquoi aller voir à l’infini ? Evidemment, il y a l’injonction poétique [1] Infini, montre un peu tes papiers ! Mais l’injonction poétique n’engage pas encore le mathématicien. Plus intriguante pour le géomètre est la nécessité de l’introduction de la perspective pour représenter dans le plan des figures dans l’espace, utilisée depuis au moins le mathématicien et peintre Piero della Francesca.
Observons la photographie ci-dessous, les droites parallèles ont l’air de se couper au loin, à l’infini [2]. Pieds de lavande sous la neige Ainsi, dans cette vue ci-dessous du Palazzo Spada par Francesco Borromini, le peintre introduit un point de fuite qui permet de reproduire cette illusion des droites parallèles qui se coupent à l’infini. Palazzo Spada Nous verrons ici que pour les mathématiciens, ce n’est pas une illusion. Avant de regarder ce qui se passe à l’infini dans un plan, regardons d’abord ce qui se passe à l’infini sur une droite, où la situation est plus simple. Pascal's Mystic Hexagon. Orthogonal Trajectories. PlanetMath.