

6 Websites To Help You Pass Coding Interviews. Understanding recursion, memoization, and dynamic programming: 3 sides of the same coin. Understanding recursion, memoization, and dynamic programming: 3 sides of the same coin Fabian Terh Oct 14, 2019 · 6 min read I previously wrote an article on solving the Knapsack Problem with dynamic programming.
In that article, I pretty much skipped to the dynamic programming solution directly, with only a brief introduction of what dynamic programming is and when it can be applied. To keep reading this story, get the free app or log in. Read the rest of this story with a free account. You’ll also discover more fresh thinking personalized to your interests and can follow your favorite authors, publications, and topics. My favorite free courses to learn data structures and algorithms in depth. How to improve your data structures, algorithms, and problem-solving skills. This post draws on my personal experiences and challenges over the past term at school, which I entered with hardly any knowledge of DSA (data structures and algorithms) and problem-solving strategies.
As a self-taught programmer, I was a lot more familiar and comfortable with general programming, such as object-oriented programming, than with the problem-solving skills required in DSA questions. This post reflects my journey throughout the term and the resources I turned to in order to quickly improve my data structures, algorithms, and problem-solving skills. I faced this issue early in the term when I didn’t know what I didn’t know, which is a particularly pernicious problem. I understood the theory well enough — for instance, what a linked list was, how it worked, its various operations and their time complexities, the ADTs (abstract data types) it supported, and how the ADT operations were implemented.
The different types of questions Knowledge of data structures You get the idea. 50+ Data Structure and Algorithms Interview Questions for Programmers. @javinpaulJavin Paul. 10 Data Structure, Algorithms, and Programming Courses to Crack Any Coding Interview. Many junior developers dream of making it at one of the larger tech companies, but, to be honest with you, getting your first job is never easy.
It is, in fact, one of the hardest things in your life and you need to put your best effort to find a job in your dream company. Most of the computer science graduates dream of working for Google, Facebook, Amazon, Microsoft, and Apple but only a few programmers clear their difficult coding interviews. The single most important reason for failing those coding job interviews is the lack of knowledge and practice. It pretty obvious that if you don’t know what to learn then you are bound to fail, hence it becomes increasingly important that you prepare hard in advance. Binary Search Algorithm in Java. 1.

Overview In this article, we'll cover advantages of a binary search over a simple linear search and walk through its implementation in Java. 2. Need for Efficient Search Let's say we're in the wine-selling business and millions of buyers are visiting our application every day. How to Merge K Sorted Arrays. With a Min-Heap. A common problem most programmers are probably familiar with is to merge two sorted arrays into a single sorted array.

It’s actually one of the earliest problems we teach here at Outco during week 1. The approach is fairly straightforward and just involves using two pointers to find the next largest element between the two arrays, and adding that to the final result. The amount of time needed just depends on how many elements there are in the two arrays, and aside from the result array, you’ll only need two pointers to keep track of where you are in each array. Input: [1, 3, 5, 7], [2, 4, 6, 8]Output: [1, 2, 3, 4, 5, 6, 7, 8] But what if the number of arrays was variable? Shunting-yard algorithm. In computer science, the shunting-yard algorithm is a method for parsing mathematical expressions specified in infix notation.
It can produce either a postfix notation string, also known as Reverse Polish notation (RPN), or an abstract syntax tree (AST). The algorithm was invented by Edsger Dijkstra and named the "shunting yard" algorithm because its operation resembles that of a railroad shunting yard. Dijkstra first described the Shunting Yard Algorithm in the Mathematisch Centrum report MR 34/61. The shunting-yard algorithm was later generalized into operator-precedence parsing.
What are stack based calculators? Stacks has many applications starting from memory management to real life and it is a fundamental (and simple) data structure that must be understood by every single software engineer.
In this article we are going to talk about how arithmetic expressions are evaluated using a Stack. A standard way of writing an arithmetic expression is called infix notation. It is a usual way of how we all are used to write arithmetic expressions: operators are placed in operands and parentheses are used to denote precedence. In postfix notation operators follow their operands and surprisingly no parentheses are needed to denote precedence. This notation is also called reverse Polish notation since it is a reverse form of Polish notation which was invented by a Polish logician and philosopher Jan Łukasiewicz and in which operators precede the operands (e.g. +34). Using a Stack we can evaluate any postfix expression very easily.
Read the expression from left to rightIf current element is a value (e.g. Different Types of Binary Tree with colourful illustrations. Shunting-yard algorithm. Structured program theorem. Graphical representation of the three basic patterns of the structured program theorem — sequence, selection, and repetition — using NS diagrams (blue) and flow charts (green).

Control flow graphs with 3 types of control structures can compute any computable function The structured program theorem, also called the Böhm–Jacopini theorem,[1][2] is a result in programming language theory. It states that a class of control flow graphs (historically called flowcharts in this context) can compute any computable function if it combines subprograms in only three specific ways (control structures). These are Executing one subprogram, and then another subprogram (sequence)Executing one of two subprograms according to the value of a boolean expression (selection)Repeatedly executing a subprogram as long as a boolean expression is true (iteration) Origin and variants[edit] Harel also writes that the more generic name was proposed by H.D. Single-while-loop, folk version of the theorem[edit] What are the top 10 algorithms every software engineer should know by heart? When you write a code, you basically provide a solution in the form of a program.
Algorithms help in reaching a right decision or providing a right solution. Knowledge and intuition regarding algorithms can greatly help you in coding. Algorithm. Flow chart of an algorithm (Euclid's algorithm) for calculating the greatest common divisor (g.c.d.) of two numbers a and b in locations named A and B.
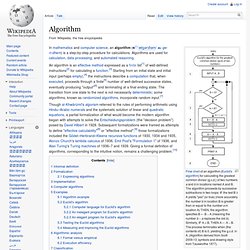
The algorithm proceeds by successive subtractions in two loops: IF the test B ≥ A yields "yes" (or true) (more accurately the numberb in location B is greater than or equal to the numbera in location A) THEN, the algorithm specifies B ← B − A (meaning the number b − a replaces the old b). Similarly, IF A > B, THEN A ← A − B. The process terminates when (the contents of) B is 0, yielding the g.c.d. in A. (Algorithm derived from Scott 2009:13; symbols and drawing style from Tausworthe 1977).
Software Engineering Must Know: Algorithms. In part 1 I reviewed must know data structures for software engineers. Part 2 focuses on must know algorithms. This is useful knowledge if you are interviewing at any big tech company or simply want to hone your skills. This list is not meant to be exhaustive, or even to cover all common algorithms you may encounter in an interview or the real world. Instead these are basic algorithms that I felt are worth committing to memory to build upon for more complicated problems. Most importantly, remember the structure of the algorithms, rather than the code verbatim.
Key concepts for sorting: Stable sorts maintain the order of elements of the same value. i.e. if “7” appears twice in the list, after sorting the two 7’s are in the same order.Divide and Conquer: Splits a data structure (usually an array) in half or by a pivot point, and recursively splits those halves to perform a sort. Bubble Sort. Archived Problems - Project Euler. Crible d'Ératosthène. Un article de Wikipédia, l'encyclopédie libre. Le crible d'Ératosthène est un procédé qui permet de trouver tous les nombres premiers inférieurs à un certain entier naturel donné N. Le crible d'Atkin est plus rapide mais plus complexe.
Algorithme[modifier | modifier le code] En supprimant tous ces multiples, à la fin il ne restera que les entiers qui ne sont multiples d'aucun entier à part 1 et eux-mêmes, et qui sont donc les nombres premiers. On commence par rayer les multiples de 2, puis les multiples de 3 restants, puis les multiples de 5 restants, et ainsi de suite en rayant à chaque fois tous les multiples du plus petit entier restant. On peut s'arrêter lorsque le carré du plus petit entier restant est supérieur au plus grand entier restant, car dans ce cas, tous les non-premiers ont déjà été rayés précédemment. À la fin du processus, tous les entiers qui n'ont pas été rayés sont les nombres premiers inférieurs à N. L'animation ci-dessous illustre le crible d'Ératosthène pour N=120 : .
Sorting algorithm. The output is in nondecreasing order (each element is no smaller than the previous element according to the desired total order);The output is a permutation (reordering) of the input. Further, the data is often taken to be in an array, which allows random access, rather than a list, which only allows sequential access, though often algorithms can be applied with suitable modification to either type of data. Since the dawn of computing, the sorting problem has attracted a great deal of research, perhaps due to the complexity of solving it efficiently despite its simple, familiar statement. For example, bubble sort was analyzed as early as 1956.[1] A fundamental limit of comparison sorting algorithms is that they require linearithmic time – O(n log n) – in the worst case, though better performance is possible on real-world data (such as almost-sorted data), and algorithms not based on comparison, such as counting sort, can have better performance.
Classification[edit] Stability[edit] means.