

JEAN MICHEL DUCANCELLE / DESIGNER. Geodesic dome. Typically a geodesic dome design begins with an icosahedron inscribed in a hypothetical sphere, tiling each triangular face with smaller triangles, then projecting the vertices of each tile to the sphere.
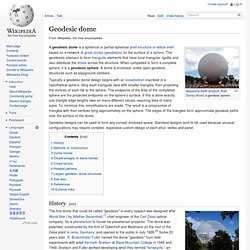
The endpoints of the links of the completed sphere are the projected endpoints on the sphere's surface. If this is done exactly, sub-triangle edge lengths take on many different values, requiring links of many sizes. To minimize this, simplifications are made. The result is a compromise of triangles with their vertices lying approximately on the sphere. The edges of the triangles form approximate geodesic paths over the surface of the dome. Geodesic designs can be used to form any curved, enclosed space. History[edit] Dome géodésique. DÔME GÉODÉSIQUEGeodesic dome, Geodätischer Dom On désigne par dômes géodésiques les polyèdres.inscriptibles à faces triangulaires et sommets de degrés 5 ou 6, ainsi que les polyèdres duaux de ces derniers, autrement dit les polyèdres circonscriptibles à sommets de degré 3 et à faces hexagonales ou pentagonales.
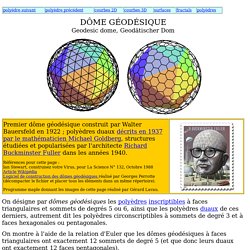
On montre à l'aide de la relation d'Euler que les dômes géodésiques à faces triangulaires ont exactement 12 sommets de degré 5 (et que donc leurs duaux ont exactement 12 faces pentagonales). Voici une méthode due à M. Goldberg, D. Richard Buckminster Fuller. Walther Bauersfeld. Walther Bauersfeld (23 January 1879 in Berlin – 28 October 1959 in Heidenheim an der Brenz) was a German engineer, employed by the Zeiss Corporation, who, on a suggestion by the German astronomer Max Wolf, started work on the first projection planetarium in 1912.
This work was stopped by military needs during World War I, but resumed after the war. Bauersfeld completed the first planetarium, known as the Zeiss I model in 1923, and it was initially placed on the roof of a Zeiss building in the corporate headquarters town of Jena.[1] This model projected 4,900 stars, and was limited to showing the sky only from Jena's latitude. Subsequently, Bauersfeld developed the Model 2 with 8,956 stars, and full latitude capability.
Over a dozen were installed before World War II again suspended planetarium work. Building a wooden geodesic dome greenhouse frame. Geodesic dome. Typically a geodesic dome design begins with an icosahedron inscribed in a hypothetical sphere, tiling each triangular face with smaller triangles, then projecting the vertices of each tile to the sphere.
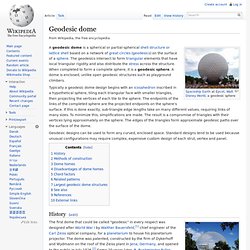
The endpoints of the links of the completed sphere are the projected endpoints on the sphere's surface. If this is done exactly, sub-triangle edge lengths take on many different values, requiring links of many sizes. To minimize this, simplifications are made. The result is a compromise of triangles with their vertices lying approximately on the sphere. The edges of the triangles form approximate geodesic paths over the surface of the dome. Geodesic designs can be used to form any curved, enclosed space. History[edit] Animation depicting Fuller's geometric explorations - Whitney Museum.
Sphère armillaire. Un article de Wikipédia, l'encyclopédie libre.
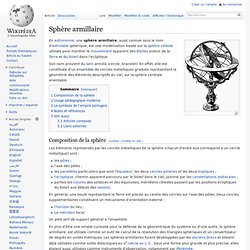
En astronomie, une sphère armillaire, aussi connue sous le nom d'astrolabe sphérique, est une modélisation basée sur la sphère céleste utilisée pour montrer le mouvement apparent des étoiles autour de la Terre et du Soleil dans l'écliptique. Son nom provient du latin armilla (cercle, bracelet). En effet, elle est constituée d'un ensemble de cercles métalliques gradués représentant la géométrie des éléments descriptifs du ciel, sur la sphère centrale orientable. Design Idea & Image Galleries on Dornob. Floating House on Behance. Floating Dome Home: Off-the-Grid Geodesic Island Retreat. On its maiden voyage, this first-of-its-kind floating dome dwelling drifted lazily between Hamburg and Berlin and certainly made waves alongside Zendome‘s general release of Home Edition, its residential variant.
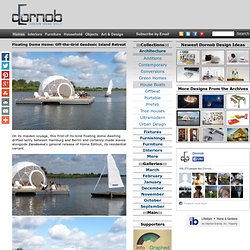
Set upon a platform of welded frame-hull construction, it blends elements of a basic dock (easy to attach a sailboat to, for instance) and an outdoor deck to compliment the PVC-and-aluminum living and sleeping zone. Naturally stable due to its lightweight construction and low center of gravity, the dome itself easily weathered its trip, though for longer cruises on more open waters (rather than peaceful rivers) it is hard to say how it would really hold up. Expandable_Habitat_Technology_Demo_for_Lunar_and_Antarctic_Applications.pdf (Objet application/pdf) DENIS OUDENDIJK.
Capsulehotel. User:Vincecate/BallHouse - Seasteading. From Seasteading Idea Idea is that a ball shape seems to ride waves really well and provide the best internal volume to surface area ratio possible.
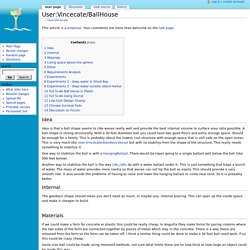
A ball shape is strong structurally. With a 30 foot diameter ball you could have two good floors and extra storage space. Should be enough for a family. One way to stabilize the ball is with a HangingBallast. Another way to stabilize the ball is the way Life_rafts do with a water ballast under it. Internal. User:Vincecate/GeodesicVessel - Seasteading. From Seasteading External Idea is that both a hull and roof could be 1/8th sphere geodesic domes.
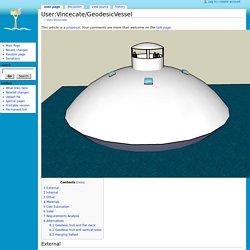
These are 80 foot in diameter in the drawing. This would sort of be a thick flying saucer shape. Video Chine : des abris sphériques pour survivre à l'apocalypse - chine, fin du monde, apocalypse. HangingBallast - Seasteading. From Seasteading Description For single-spar designs which are gravitationally stable (C_g below C_b), rather than having the ballast at the bottom of the spar, we could hang it from the spar for additional stability.
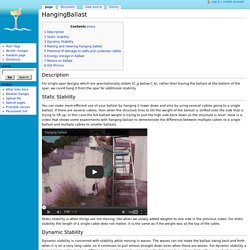
Static Stability. User:Jesrad/BunkerStead - Seasteading. From Seasteading A BunkerStead is a minimalist design for a spar seastead, where the spar does not reach high enough above the waterline to avoid having its top submerged by the taller waves.
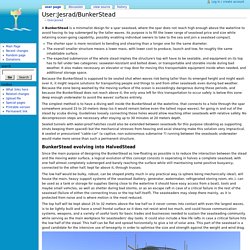
Its purpose is to fill the lower range of seastead price and size while retaining ocean-going capability, possibly enabling individual owners to take to the sea and join a seastead compact. The shorter spar is more resistant to bending and shearing than a longer one for the same diameter. The overall smaller structure means a lower mass, with lower cost to produce, launch and tow, for roughly the same inhabitable surface. The expected submersion of the whole stead implies the structure's top will have to be sealable, and equipment on its top has to fall under two categories: seawater-resistant and bolted down, or transportable and storable inside during bad weather. Acconci Studio. Old School⎢Wenzel Jamnitzer I « Je vous prendrai un Viennois à emporter s’il vous plaît. » Comme son prénom ne l’indique pas, Wenzel était un « warmes kaninchen », tenez-le vous pour dit.
Il a fait 7 garçons et 4 filles à sa femme, Anna Braunreuchin. En même temps, à cette époque là, il fallait bien s’occuper et se réchauffer l’hiver et quoi de mieux que la chaleur de la lourde poitrine et la douceur des bonnes cuisses velues (je vous rappelle que nous nous trouvons au XVIe siècle) de sa femme pour ça ? Géode (géométrie) Un article de Wikipédia, l'encyclopédie libre. Pour les articles homonymes, voir Géode. Géode par triangulation Géode en nid d'abeille La plupart des géodes sont bâties sur le principe suivant : on part d'un icosaèdre. Tutorial #3: The icosahedron-based geodesic sphere. The content that follows was originally published on the Don Havey website at This quick tutorial will show a more reasonable alternative to the electronsphere, which addressed the problem of distributing points evenly on a sphere.
We’ll be creating a geodesic sphere (like at the Epcot center) using a subdivided icosahedron. It’s a relatively simple script and inexpensive in terms of CPU usage. Much more efficient than the electronsphere approach, though not quite as interesting. And here are the classes you’ll need: Icosahedron classes About the geodesic sphere The geodesic dome and sphere are often credited to Buckminster Fuller, although it is generally acknowledged that he did not invent the shape or concept, but rather investigated and expanded upon them.
Solide de Platon. Un article de Wikipédia, l'encyclopédie libre. En géométrie euclidienne, un solide de Platon est un polyèdre régulier et convexe. Entre les polygones réguliers et convexes de la géométrie plane, et les polyèdres réguliers convexes de l’espace à trois dimensions, il y a une analogie, mais aussi une différence notable. Solide de Johnson. Cuboctaedre.