

The quilted universe. The Inflationary universe. Eternal inflation. Eternal inflation is predicted by many different models of cosmic inflation.
MIT professor Alan H. Guth proposed an inflation model involving a "false vacuum" phase with positive vacuum energy. Parts of the Universe in that phase inflate, and only occasionally decay to lower-energy, non-inflating phases or the ground state. The Brane multiverse. Brane cosmology. Brane cosmology refers to several theories in particle physics and cosmology related to string theory, superstring theory and M-theory.
Brane and bulk[edit] The central idea is that the visible, four-dimensional universe is restricted to a brane inside a higher-dimensional space, called the "bulk" (also known as "hyperspace"). If the additional dimensions are compact, then the observed universe contains the extra dimensions, and then no reference to the bulk is appropriate.
In the bulk model, at least some of the extra dimensions are extensive (possibly infinite), and other branes may be moving through this bulk. Interactions with the bulk, and possibly with other branes, can influence our brane and thus introduce effects not seen in more standard cosmological models. The Cyclic multiverse. Cyclic model. A cyclic model (or oscillating model) is any of several cosmological models in which the universe follows infinite, or indefinite, self-sustaining cycles.

For example, the oscillating universe theory briefly considered by Albert Einstein in 1930 theorized a universe following an eternal series of oscillations, each beginning with a big bang and ending with a big crunch; in the interim, the universe would expand for a period of time before the gravitational attraction of matter causes it to collapse back in and undergo a bounce. Overview[edit] In the 1920s, theoretical physicists, most notably Albert Einstein, considered the possibility of a cyclic model for the universe as an (everlasting) alternative to the model of an expanding universe. However, work by Richard C. Tolman in 1934 showed that these early attempts failed because of the cyclic problem: according to the Second Law of Thermodynamics, entropy can only increase.[1] This implies that successive cycles grow longer and larger. The Landscape multiverse.
String theory landscape. The string theory landscape refers to the huge number of possible false vacua in string theory.[1] The large number of theoretically allowed configurations has prompted suggestions that certain physical mysteries, particularly relating to the fine-tuning of constants like the cosmological constant or the Higgs boson mass, may be explained not by a physical mechanism but by assuming that many different vacua are physically realized.[2] The anthropic landscape thus refers to the collection of those portions of the landscape that are suitable for supporting intelligent life, an application of the anthropic principle that selects a subset of the otherwise possible configurations.
Anthropic principle[edit] Bayesian probability[edit] Some physicists, starting with Weinberg, have proposed that Bayesian probability can be used to compute probability distributions for fundamental physical parameters, where the probability of observing some fundamental parameters is given by, where and . The Quantum multiverse. Many-worlds interpretation. The quantum-mechanical "Schrödinger's cat" paradox according to the many-worlds interpretation.
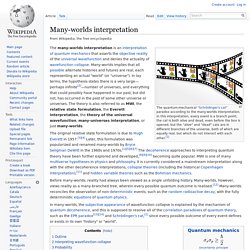
In this interpretation, every event is a branch point; the cat is both alive and dead, even before the box is opened, but the "alive" and "dead" cats are in different branches of the universe, both of which are equally real, but which do not interact with each other.[1] The Holographic multiverse. Holographic principle. In a larger sense, the theory suggests that the entire universe can be seen as a two-dimensional information structure "painted" on the cosmological horizon[clarification needed], such that the three dimensions we observe are an effective description only at macroscopic scales and at low energies.
Cosmological holography has not been made mathematically precise, partly because the particle horizon has a finite area and grows with time.[4][5] The holographic principle was inspired by black hole thermodynamics, which conjectures that the maximal entropy in any region scales with the radius squared, and not cubed as might be expected. The Simulated multiverse. Simulated reality. Simulated reality is the hypothesis that reality could be simulated—for example by computer simulation—to a degree indistinguishable from "true" reality.
It could contain conscious minds which may or may not be fully aware that they are living inside a simulation. This is quite different from the current, technologically achievable concept of virtual reality. Virtual reality is easily distinguished from the experience of actuality; participants are never in doubt about the nature of what they experience.
Simulated reality, by contrast, would be hard or impossible to separate from "true" reality. There has been much debate over this topic, ranging from philosophical discourse to practical applications in computing. The Ultimate multiverse. Mathematical universe hypothesis. In physics and cosmology, the mathematical universe hypothesis (MUH), also known as the Ultimate Ensemble, is a speculative "theory of everything" (TOE) proposed by the cosmologist Max Tegmark.[1][2] Description[edit] Tegmark's mathematical universe hypothesis (MUH) is: Our external physical reality is a mathematical structure.
That is, the physical universe is mathematics in a well-defined sense, and "in those [worlds] complex enough to contain self-aware substructures [they] will subjectively perceive themselves as existing in a physically 'real' world".[3][4] The hypothesis suggests that worlds corresponding to different sets of initial conditions, physical constants, or altogether different equations may be considered equally real. Tegmark elaborates the MUH into the Computable Universe Hypothesis (CUH), which posits that all computable mathematical structures (in Godel's sense) exist.[5] Tegmark claims that the hypothesis has no free parameters and is not observationally ruled out.