

Exploration de données. Un article de Wikipédia, l'encyclopédie libre.
Vous lisez un « bon article ». L'utilisation industrielle ou opérationnelle de ce savoir dans le monde professionnel permet de résoudre des problèmes très divers, allant de la gestion de la relation client à la maintenance préventive, en passant par la détection de fraudes ou encore l'optimisation de sites web. C'est aussi le mode de travail du journalisme de données[1]. L'exploration de données[2] fait suite, dans l'escalade de l'exploitation des données de l'entreprise, à l'informatique décisionnelle.
Histoire[modifier | modifier le code] Collecter les données, les analyser et les présenter au client. De 1919 à 1925, Ronald Fisher met au point l'analyse de la variance comme outil pour son projet d'inférence statistique médicale. L'arrivée progressive des micro-ordinateurs permet de généraliser facilement ces méthodes bayésiennes sans grever les coûts. Applications industrielles[modifier | modifier le code]
Règles d'Association. Algorithme APriori. Un article de Wikipédia, l'encyclopédie libre.
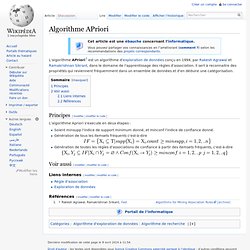
L'algorithme APriori[1] est un algorithme d'exploration de données conçu en 1994, par Rakesh Agrawal et Ramakrishnan Sikrant, dans le domaine de l'apprentissage des règles d'association. Il sert à reconnaitre des propriétés qui reviennent fréquemment dans un ensemble de données et d'en déduire une catégorisation. Principes[modifier | modifier le code] Global Reporting Initiative. Un article de Wikipédia, l'encyclopédie libre.
Pour les articles homonymes, voir GRI. Le Global Reporting Initiative (GRI) a été établi vers la fin 1997 avec comme mission de développer les directives applicables mondialement en matière de développement durable, ainsi que de rendre compte des performances économiques, environnementales et sociales, initialement pour des sociétés puis, par la suite, pour n'importe quelle organisation gouvernementale ou non gouvernementale. Rassemblée par la coalition pour les économies environnementalement responsables (CERES) en association avec le programme d'environnement des Nations Unies (PNUE), le GRI incorpore la participation active des sociétés, des O.N.G., des organismes de comptabilité, des associations d'hommes d'affaires, et d'autres parties prenantes du monde entier.
La version GRI actuellement en vigueur (depuis 2013) se nomme G4. Elle est appelée à remplacer progressivement les lignes directrices G3 et G3.1. Par importance : Par domaine : PageRank. Un article de Wikipédia, l'encyclopédie libre. Illustration du PageRank. Le PageRank[note 1] ou PR est l'algorithme d'analyse des liens concourant au système de classement des pages Web utilisé par le moteur de recherche Google. Il mesure quantitativement la popularité d'une page web.
Partitionnement. K-means. Un article de Wikipédia, l'encyclopédie libre.
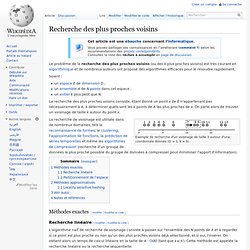
Le problème de la recherche des plus proches voisins (ou des k plus proches voisins) est très courant en algorithmique et de nombreux auteurs ont proposé des algorithmes efficaces pour le résoudre rapidement. Soient : La recherche des plus proches voisins consiste, étant donné un point x de E n'appartenant pas nécessairement à A, à déterminer quels sont les k points de A les plus proches de x. K-médoïdes. Un article de Wikipédia, l'encyclopédie libre.
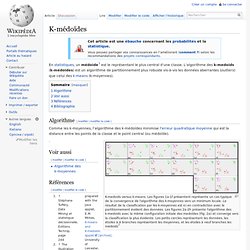
En statistiques, un médoïde[1] est le représentant le plus central d'une classe. L'algorithme des k-medoids (k-médoïdes) est un algorithme de partitionnement plus robuste vis-à-vis les données aberrantes (outliers) que celui des k-means (k-moyennes). Algorithme[modifier | modifier le code] Comme les k-moyennes, l'algorithme des k-médoïdes minimise l'erreur quadratique moyenne qui est la distance entre les points de la classe et le point central (ou médoïde).
K-medoids versus k-means. Voir aussi[modifier | modifier le code] Réseau de neurones artificiels. Un article de Wikipédia, l'encyclopédie libre.
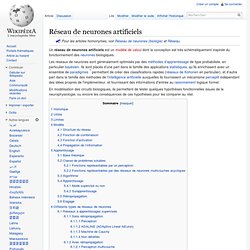
Un réseau de neurones artificiels est un modèle de calcul dont la conception est très schématiquement inspirée du fonctionnement des neurones biologiques. Les réseaux de neurones sont généralement optimisés par des méthodes d’apprentissage de type probabiliste, en particulier bayésien. Ils sont placés d’une part dans la famille des applications statistiques, qu’ils enrichissent avec un ensemble de paradigmes [1] permettant de créer des classifications rapides (réseaux de Kohonen en particulier), et d’autre part dans la famille des méthodes de l’intelligence artificielle auxquelles ils fournissent un mécanisme perceptif indépendant des idées propres de l'implémenteur, et fournissant des informations d'entrée au raisonnement logique formel.
En modélisation des circuits biologiques, ils permettent de tester quelques hypothèses fonctionnelles issues de la neurophysiologie, ou encore les conséquences de ces hypothèses pour les comparer au réel. Algorithme espérance-maximisation. Un article de Wikipédia, l'encyclopédie libre.
L' (en anglais , souvent abrégé ), proposé par Dempster et al. (1977) [ 1 ] , est une classe d' algorithmes qui permettent de trouver le maximum de vraisemblance des paramètres de modèles probabilistes lorsque le modèle dépend de variables latentes non observables. On utilise souvent l'algorithme EM pour la classification de données, l'apprentissage automatique, ou la vision artificielle. On peut également citer son utilisation en imagerie médicale dans le cadre de la reconstruction tomographique. AdaBoost. Un article de Wikipédia, l'encyclopédie libre.
Adaboost (ou adaptive boosting) est une méthode de boosting (intelligence artificielle, apprentissage automatique) introduite par Yoav Freund et Robert Schapire (Freund et Schapire 1997). Histoire et principe[modifier | modifier le code] Ce fut l'une des premières méthodes pleinement fonctionnelles permettant de mettre en œuvre le principe de boosting. Les auteurs ont reçu le prestigieux prix Gödel en 2003 pour leur découverte[1].
Regroupement hiérarchique. Un article de Wikipédia, l'encyclopédie libre.
Dans le domaine informatique, et plus précisément dans le domaine de l'analyse et de la classification automatique de données, la notion de regroupement hiérarchique recouvre différentes méthodes de clustering, c'est-à-dire de classification par algorithme de classification. La classification ascendante hiérarchique (CAH)[modifier | modifier le code] Analyse discriminante. Un article de Wikipédia, l'encyclopédie libre.
L’analyse factorielle discriminante ou analyse discriminante est une technique statistique qui vise à décrire, expliquer et prédire l’appartenance à des groupes prédéfinis (classes, modalités de la variable à prédire, …) d’un ensemble d’observations (individus, exemples, …) à partir d’une série de variables prédictives (descripteurs, variables exogènes, …). L’analyse discriminante est utilisée dans de nombreux domaines : En médecine, par exemple pour détecter les groupes à hauts risques cardiaques à partir de caractéristiques telles que l’alimentation, le fait de fumer ou pas, les antécédents familiaux, etc.Dans le domaine bancaire, lorsque l’on veut évaluer la fiabilité d’un demandeur de crédit à partir de ses revenus, du nombre de personnes à charge, des encours de crédits qu’il détient, etc.En biologie, lorsque l’on veut affecter un objet à sa famille d’appartenance à partir de ses caractéristiques physiques.
Observations décrites par. Méthode Condorcet. Un article de Wikipédia, l'encyclopédie libre. La méthode Condorcet (ou vote Condorcet) est un système de vote dans lequel l'unique vainqueur est celui, s'il existe, qui, comparé tour à tour à tous les autres candidats, s'avérerait à chaque fois être le candidat préféré. Rien ne garantit la présence d'un candidat satisfaisant à ce critère. Ainsi, tout système de vote fondé sur la méthode comparative de Condorcet doit prévoir un moyen de résoudre les votes pour lesquels ce candidat idéal n'existe pas. Cette méthode doit son nom au marquis de Condorcet, mathématicien et philosophe français du XVIIIe siècle, bien que la méthode fût déjà connue de l'écrivain catalan Raymond Lulle (1299).
Motivation[modifier | modifier le code] Dans son Essai sur l'application de l'analyse à la probabilité des décisions rendues à la pluralité des voix, Condorcet met en évidence le fait que le vote à la pluralité peut très bien ne pas représenter les désirs des électeurs.
AFC - Analyse factorielle des correspondances. Un article de Wikipédia, l'encyclopédie libre. Pour les articles homonymes, voir AFC. L'analyse factorielle des correspondances, en abrégée AFC, est une méthode statistique d'analyse des données mise au point par Jean-Paul Benzecri alors professeur à la faculté des sciences de Rennes[1]. Par la suite, il fut professeur à l'Université Pierre-et-Marie-Curie à Paris (ISUP et Laboratoire de statistique multidimensionnelle). Introduction[modifier | modifier le code] Dit grossièrement, une méthode AFC admet en entrée un "tableau croisé dynamique", et produit en sortie une ou plusieurs cartes ou images de répartition des valeurs et des variables.
La technique de l'AFC est essentiellement utilisée pour de grands tableaux de données toutes comparables entre elles (si possible exprimées toutes dans la même unité, comme une monnaie, une dimension, une fréquence ou toute autre grandeur mesurable). Principe[modifier | modifier le code] ACM - Analyse des correspondances multiples. Un article de Wikipédia, l'encyclopédie libre. Pour les articles homonymes, voir ACM. L’analyse des correspondances multiples (ACM) est la méthode factorielle (au sens français du terme) adaptée aux tableaux dans lesquels un ensemble d’individus (en lignes) est décrit par un ensemble de variables qualitatives (en colonnes). ACP - Analyse en composantes principales. Un article de Wikipédia, l'encyclopédie libre. Pour les articles homonymes, voir ACP.
L'Analyse en composantes principales (ACP) est une méthode de la famille de l'analyse des données et plus généralement de la statistique multivariée, qui consiste à transformer des variables liées entre elles (dites "corrélées" en statistique) en nouvelles variables décorrélées les unes des autres. Ces nouvelles variables sont nommées "composantes principales", ou axes principaux. Analyse en composantes indépendantes. Positionnement multidimensionnel.
Méthode CRISP-DM. SEMMA. Six Sigma. Un article de Wikipédia, l'encyclopédie libre. La méthode Six Sigma se base sur une démarche fondée à la fois sur la voix du client (enquêtes, etc.) et sur des données mesurables (par indicateurs) et fiables.