

Loi universelle de la gravitation. Un article de Wikipédia, l'encyclopédie libre.
Les satellites et les projectiles obéissent à la même loi. Expression mathématique selon Isaac Newton[modifier | modifier le code] Deux corps ponctuels de masses respectives et s'attirent avec des forces de mêmes valeurs (mais vectoriellement opposées), proportionnelles à chacune des masses, et inversement proportionnelle au carré de la distance qui les sépare.
La force exercée sur le corps par le corps est vectoriellement donnée par en kilogramme (kg); d en mètre (m); en newton (N) où G est la constante gravitationnelle, elle vaut dans les unités SI, le CODATA 2010 [2] Énergie potentielle de gravitation[modifier | modifier le code] Voici le calcul menant à l'expression de l'énergie potentielle de gravitation d'un corps de masse m à une distance R d'un corps de masse M produisant le champ de gravitation : D'où : Énergie potentielle d'une sphère homogène[modifier | modifier le code] Soit un corps sphérique de rayon R et de masse volumique uniforme , on a : Constante gravitationnelle. Un article de Wikipédia, l'encyclopédie libre.
En physique, la constante de proportionnalité de la loi de la gravitation est notée , et est appelée constante gravitationnelle, ou constante universelle de gravitation, ou constante de Newton[1], ou constante de Cavendish[2], ou plus simplement grand G[3]. La constante gravitationnelle est une constante physique fondamentale qui apparaît dans la loi d'Isaac Newton sur la gravitation universelle et les lois qui en découlent (lois de Kepler, etc.).
La constante gravitationnelle apparaît aussi dans la théorie de la relativité générale d'Albert Einstein. Contrairement à d'autres constantes physiques, il n'existe pas de valeur de G qui soit exacte par définition. Mise en évidence[modifier | modifier le code] En analyse dimensionnelle, la dimension d'une force est : La dimension de est : L'équation aux dimensions reliant à doit faire intervenir un facteur de dimension : Ce facteur est de sorte que : Notation[modifier | modifier le code] D'après John J. Et. Paramètre gravitationnel standard. Un article de Wikipédia, l'encyclopédie libre.
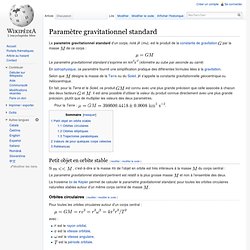
Le paramètre gravitationnel standard d'un corps, noté (mu), est le produit de la constante de gravitation par la masse de ce corps : Le paramètre gravitationnel standard s'exprime en km3s-2 (kilomètre au cube par seconde au carré) En astrophysique, ce paramètre fournit une simplification pratique des différentes formules liées à la gravitation. Selon que désigne la masse de la Terre ou du Soleil, s'appelle la constante gravitationnelle géocentrique ou héliocentrique. En fait, pour la Terre et le Soleil, ce produit est connu avec une plus grande précision que celle associée à chacun des deux facteurs et .
Pour la Terre : Petit objet en orbite stable[modifier | modifier le code] Si , c'est-à-dire si la masse. Evaluations des masses de l'univers. Newton (1642 / 1722) Newton reprend l'idée de Tycho Brahé selon laquelle les objets sont "maintenus dans la sphère céleste par une force divine".

Par analogie avec le mouvement d'une pierre tenue par une fronde puis lâchée soudainement, il comprend que la Lune, par exemple, "tombe" à chaque instant sur la Terre, sous l'influence d'une force qui dépend de la masse m de la Lune, de la masse M de la Terre, et de leur distance d : Partant de cette formule, il démontre que la trajectoire de la Lune est nécessairement elliptique. Aussi quand l'astronome Halley vient lui demander de l'aide pour calculer la trajectoire de sa fameuse comète, sa réponse est déjà prête. Halley le pousse à publier. Malheureusement, on ne connaît pas la constante de gravitation G : Newton parvient à l'éliminer quand il compare deux planètes, et compte tenu du fait que la masse M du soleil est considérablement plus importante que celle des planètes : Cavendish (1731 / 1810) Montrer que le travail de la force de gravitation est l'opposée de la variation d'énergie potentielle Ep=-G mMT / r. (r : distan.